When students are looking at story problems, they’ll typically do one of two things.

They might scan through the problem, circle the numbers and underline the key words like all together or difference. If the class is working on adding that week, then they will add the numbers, if they’re subtracting that week, they’ll subtract the numbers. In this situation, students don’t know mathematically what the problem is actually asking them so they do a lot of guessing and checking.
In another scenario, students might just give up or appeal to a teacher for help. They just wait for someone to help them or just give up because it’s too complex. Honestly, who can blame them? Sometimes when you’re reading a story problem, there are so many words they just start swimming in front of you. Today, kids need a lot of help with comprehension of math problems, with understanding what a problem is actually asking them to do. The words of the problem circle in their heads and they don’t have a visual reference for understanding what the problem is asking.
 Often when we go into classrooms, especially in lower elementary, we’ll see this classic T-chart. There’s a plus sign on one side of the chart and a minus sign on the other side. On the plus side, there are vocabulary words like sum, all together, in all, and then on the subtraction side, there are words like difference, how many more than, subtract. It’s not a bad thing do to a T-chart like this because we certainly want students to understand what the actual vocabulary is asking. But often, we don’t realize that this type of vocabulary is only representative of ⅕ of the type of problems that kids will encounter in elementary school.
Often when we go into classrooms, especially in lower elementary, we’ll see this classic T-chart. There’s a plus sign on one side of the chart and a minus sign on the other side. On the plus side, there are vocabulary words like sum, all together, in all, and then on the subtraction side, there are words like difference, how many more than, subtract. It’s not a bad thing do to a T-chart like this because we certainly want students to understand what the actual vocabulary is asking. But often, we don’t realize that this type of vocabulary is only representative of ⅕ of the type of problems that kids will encounter in elementary school.
We want to make sure that we don’t teach conditions in math, for example, you only add if you see all together. Some kids will see those key words, and just automatically add whatever digits they see in the story problem. But that doesn’t always work. Here’s an example:
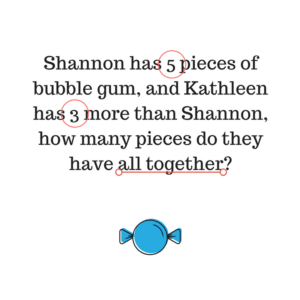
The child might circle the numbers 5 and 3, see the key words all together, and think “oh! That’s on my T-chart under the plus!” so then they just add and get 8, which is incorrect. In reality, this is an additive/comparison problem where Shannon has 5, but Kathleen also has 5, as well as an additional 3. The child should add 5 + 5 + 3 to get 13 as the correct answer. So many times, students don’t completely understand what the problem is asking because they’ve been conditioned to circle numbers and underline keywords.
Even in first grade, students are asked to be doing additive/comparison and a variety of part/whole problems. By the time students get to 3rd and 4th grade, they’re doing multiplicative/comparison problems and many multi-step problems, so their key word clues aren’t going to help.
So how are we actually teaching problem solving? Are we doing it in a systematic way that can help students independently apply these concepts on their own without a teacher present helping them, like in a testing situation? Twenty-five percent of the Next Generation Assessment will be problem solving. In 21st century math, a child will encounter a lot of application problems that will require them to know how to approach the problem without any help.
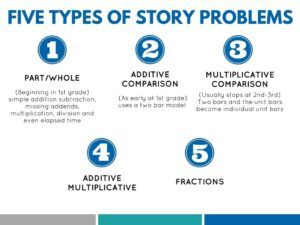
Enter: model drawing. Model drawing goes by many names: some schools call it bar models, some call it tape diagrams, and some call it action model drawings. I prefer to call it model drawing because it’s pretty universal to any kind of model you could make instead of being locked into one type of diagram that really isn’t a bar. No matter what you call it, model drawings are amazing! They were adopted from a Singaporian problem solving approach for students, beginning with proportional models to look at individual squares or units being represented, and then going throughout first grade, and taking the idea and bringing it into a actual non-proportional manipulative like a unit bar.
There are five different types of model drawings in elementary school. Over the next five blog posts, we will break down each of the type of problems to help you give a model for what they would look like. In middle school, we start to add in model drawings using ratios and proportions as well.
Resources for learning how to incorporate model drawings:
- Classroom poster. You will definitely need a step-by-step model drawing poster. This is a great poster that should be hung up in every classroom. Our project schools are required to hang one in every classroom from 1st grade up so that students see a systematic way that we do problem solving, not just in their class, but throughout the building. When students are in second grade and they’ve learned problem solving this way, it’s a quick connection to see how they’ll be problem solving in 3rd grade too. Same set of steps, different content. The idea of model drawing actually grows with students from first grade all the way through eighth grade, so you can use it as a sustained idea.
- An individual Step by Step Model Drawing Student Checklist that is next to them while they work. Even though you have a step-by-step model drawing poster at the front of your classroom, it’s important for students to have their own individual sheets next to them while they are doing problem solving as well. The poster has seven steps, and the individual sheet actually has eight steps because it goes with our journal template that we use. Kids always have to communicate their thinking, so we’ve added step eight to these individual sheets, where kids have to record an explanation of their thinking. This can be stored in a clear plastic sleeve or in a journal, or glued in the front of a math notebook.

- Journal Template: PreK or Elementary. Another essential component for model drawing is our journal template. There’s a spot for the sentence form, a spot for the model drawing, a spot for the computation, and a spot for the explanation. Teachers can insert the question at the top of the page, or students can write/paste in the question themselves before they begin. This doesn’t have to be copied and used for every single problem. Sometimes you might make a copy, but sometimes you could just say “I up your journal.” If you look at the template, it looks like the letter I with the middle part of the I moved over a bit to provide room for the model drawing. Some teachers just like the consistency of the template, so they make the copies.

- Reference Books. Step by Step Model Drawing and More Challenging Model Drawings are two great resources to support your journey into problem solving as you learn to do model drawings. Both authors do a great job of really teaching you step by step, how to get model drawings integrated into your class. These stand-alone books are intended to help you get these kinds of problems into your classroom, while the others are more of a resource for using with students.
- Resource Books. We need to become good at model drawing ourselves. Teachers are generally book-followers, we go by the directions it gives us in the books. Sometimes, however, the book doesn’t really give us a systematic way to handle story problems. Many of our teachers have to teach themselves how to do model drawings. A great way to do this at the beginning is to use our Word Problems books (one for each grade level, 1-6). We typically recommend the book for the teacher’s grade level and the one below, so if you were teaching 3rd grade, you’d get the 3rd grade book, and 2nd grade book, partly because the students are going to be as new to model drawings as you are. So, if I’m working on additive/comparison problems, I might grab a few problems from the 2nd grade book, then go into the 3rd grade book. Each book has approximately 180 story problems and is really great for kids to use and for teachers to get started.
Manipulatives
What manipulatives go with model drawings?
Let’s revisit our story problem:
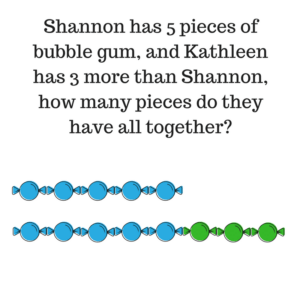
Cuisenaire Rods are really great for part/whole and additive/comparison problems. On the proportional side, a student could grab a Cuisenaire rod of five to represent what Shannon had, and the same color could be used to represent Kathleen’s five pieces. But then they could grab an additional three to tack onto the end of Kathleen’s five. We particularly like the connecting Cuisenaire rods because they allow kids to be able to interlock some of them, but in many schools, they have the block style Cuisenaire rods, and those will work just fine too.
The 1” square tiles are mainly used for multiplicative/comparison problems.

You’ll also need a Math Work Mat. Kids really need this Math Work Mat when they’re using the manipulatives because they can build their model on this space instead of in their actual journal paper. Many kids, when using manipulatives as well as pen/paper, will build their model on the paper they’re supposed to draw or put their computation on. You don’t have to use our official document, any piece of paper that students are conditioned to use as a space for building their model will work.
ThinkingBlocks.com (via the Math Playground) is another excellent resource that we like to use in our math workshop in the Math with Technology station. (We blogged about it here: Thinking Blocks) If you have Chromebooks or laptops, or even iPads (with downloadable apps), you can use this program. There are several sections available in ThinkingBlocks.com – addition problems, part/whole problems, comparison bars, multiplication, proportions, etc. One of the problems we used to have with this tool was that many of the students we were using it with couldn’t actually read the problem. But Thinking Blocks just added a new feature where you can click on a speaker icon and hear the text of the story read to you, which is huge!

Setting up for Success
As you begin to implement model drawings in your class, we recommend using model drawing and the journal templates at the minimum of 2-3 times per week. Kids need consistent structure with understanding the comprehension strategy to help them attack problems. We have seen huge growth with kids that come to us with their problems.
The most important thing is for the teacher to be patient, it will take time to learn this new language because most of us did not learn this way. We did not have a pictorial representation or even think about using any kind of concrete objects to help us master harder story problems.
Ultimately we want you to feel comfortable enough with the different types of story problems that you could look at your math series and to know which type of problem you were facing and how to do the required diagram. Not every math series uses these types of problems, but it is my strong recommendation that, even if it doesn’t, you apply these five types of problems to it. Your math book isn’t your bible, it’s a resource for you to teach your curriculum. Your curriculum is your standards. So we want to be able to apply this approach to whatever we’re using. It’s challenging to be able to look at a story problem and just know that, “Oh! This is an additive/comparison problem, so I’m going to help my kids get set up for it this way.”
Model drawing does take a lot of modeling, and it also might take you some time to go a grade level back in order to break down the problems before you bring them up in a way that students can understand.
The next few weeks on our blog, we will spend some time diving deep into each of the five areas that you would see in a classroom and some different ways to introduce them into your classroom. We hope you’ll check out our resources as well!
To celebrate our new series, we would like to offer you 10% off of the items that support model drawing with the code: SISMODEL
Check out our Model Drawing category to see all the products in one place. We also have Problem Solving Kits that are already created and ready to go for each grade level! Just click on the kit, add it to your cart, and you’ll have everything you need!



