How did you learn how to add fractions as a child?

I remember my teacher telling me to add the numerator and just keep the denominator the same. I also vividly remember asking why? Why am I adding the top number, but not the bottom number?? The teacher answered “because that’s just how you do it.”
Think about this problem: 5/7 + 6/7. The rule says add the numerators and keep the denominator the same, so I go across and add 5 + 6, keep the bottom number the same and the answer is 11/7.
Many students faced with the same problem forget about the rule for the denominator, so you might also get 11/14 as an answer. While that looks like it should be right (after all, you added the top numbers and then added the bottom numbers, right?), of course, we know that isn’t the answer at all. Teachers will tell students to go back and “do it right,” meaning “go back and follow the procedure.”
But does this procedure we’re supposed to follow actually help students understand the why before teaching them the how? Do students in your classroom really understand what’s happening when you’re adding fractions? Do they understand what that whole fraction is? Do they understand benchmark fractions as they’re adding?
In this blog we’re going to see how we can use CPA (concrete pictorial abstract) means to help our students to understand what’s going on with the addition of fractions.
Improper Fractions
Let’s go back to that problem of 5/8 + 6/8. When the procedure is followed correctly, we get 11/8. The answer is what we might call an improper fraction.
I try not to use the term improper fraction, however, because it isn’t truly improper, is it? It’s still a fraction that we could visualize – if I was really hungry and I wanted to eat 11/8 of the pizzas that were out, I could do that. Instead of calling them improper fractions, we need to make sure that students understand that an improper fraction just means a fraction larger than one. Consequently, students need to know what one whole is in any given problem to help them be successful as they continue solving.
Back to our “fraction that’s larger than one” – 11/8. The next thing the teacher says is usually, change this improper fraction into a mixed number. The student has been taught a procedure for that, so he starts to think Oh yeah, I have to figure out how many times 8 goes into 11. I think it might go in there twice, no wait, that’s too high. Let me think about it… it goes in there once, and that would be 8 and then if I count up 9, 10, 11. I’m going to put there’s a remainder of 3.
But it’s a fraction, so the teacher tells the student to write it that way. The student puts that remainder over the fractional part, and gets the answer of 1 3/8.
What we see here is that, if the student follows all the procedures, they get the answer. But I’m not convinced that student, or any students today, will really understand the why behind what they’re doing with fractions by just following procedures.
Many adults have fraction phobia as well because they weren’t comfortable using fractions when they were younger, and therefore, when they go to teach it, it comes out procedural, just like they learned it.
Simplifying Fractions
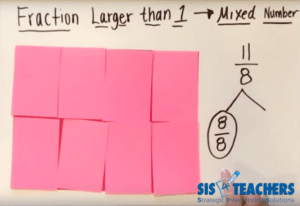 How could we could help students to easily understand taking a fraction larger than one, and changing it into a mixed number? Let’s have them think about what the fractional parts are. If we ended up having this total of 11/8, we need to know what the whole is. Since we have 8 as the denominator, we know that the whole would be equal to 8/8. Based on that, I can use what I know about decomposing from our Math Mights friend, D.C. to smash or decompose that 11/8 into a whole, which is equal to 8/8. We have students circle the 8/8 to help them remember that 8/8 is equal to one whole. If our total was 11/8, and I’m showing 8/8, how many more 8ths are left? 3/8. So the answer is 1 3/8
How could we could help students to easily understand taking a fraction larger than one, and changing it into a mixed number? Let’s have them think about what the fractional parts are. If we ended up having this total of 11/8, we need to know what the whole is. Since we have 8 as the denominator, we know that the whole would be equal to 8/8. Based on that, I can use what I know about decomposing from our Math Mights friend, D.C. to smash or decompose that 11/8 into a whole, which is equal to 8/8. We have students circle the 8/8 to help them remember that 8/8 is equal to one whole. If our total was 11/8, and I’m showing 8/8, how many more 8ths are left? 3/8. So the answer is 1 3/8
When students think of simplifying fractions this way, they can decompose fractions that are larger than one and put them into a mixed number in a way that makes more sense. In this video we’re going to show you different examples of how you can use a concrete tool when students are adding two fractions with common denominators, coming up with a fraction larger than one, and changing it into a mixed number.
CPA
When adding fractions, it’s really important that we make sure that students are understanding what we’re talking about conceptually, pictorially, and abstractly. But we don’t want to teach those things in isolation. We want to teach through CPA, meaning that kids can show different ways of understanding what they’re doing.
I like using our area model papers for students because they aren’t stamped like the fraction tiles, and they help students to conceptualize what’s actually happening as they simplify, or reduce, a fraction down to show another name of that fraction. In this video, we’re going to show how to add fractions with common denominators. I’ll also show how you could have conversations with students around their thinking based on their prior knowledge, or what they’re doing as they’re using the different parts to it.
Note: When adding fractions, we might need two of the area model kits so students can see what’s happening, especially if the total is going to be larger than one.
Adding Fractions with Common Denominators
Let’s use the example of 6/8 + 4/8. To show this in a concrete way, we want students to use their whole sheet of paper and stack their 8ths on top to show 6/8 and then add in 4 more 8ths. You could also have students work in pairs to do this simultaneously where Partner A builds 6/8 and Partner B builds 4/8.
 We want students to look and see how many more pieces we need to make a whole, which in this case is 8/8. On one paper, Partner A has 6/8 covering the whole, and on the other Partner B has 4/8 covering the whole. With the problem laid out like this, it is easy to see how you can decompose the 4/8 into 2/8 and 2/8, take 2/8 and combine it with 6/8 to make a whole, and then have 2/8 left over.
We want students to look and see how many more pieces we need to make a whole, which in this case is 8/8. On one paper, Partner A has 6/8 covering the whole, and on the other Partner B has 4/8 covering the whole. With the problem laid out like this, it is easy to see how you can decompose the 4/8 into 2/8 and 2/8, take 2/8 and combine it with 6/8 to make a whole, and then have 2/8 left over.
When kids see the problem concretely, with the area model papers, they can use a kind of fraction number bond which is a really great pictorial representation of their mathematical thinking. Then abstractly, they can show the new problem that they created through decomposing and composing, which is 1 plus 2/8.
Using decomposing and composing is a great way to show kids how to understand how to add fractions with common denominators. Check out our DC video on how DC is adding together fractions by decomposing to make the problems easier.
Adding Fractions with Uncommon Denominators
You can also use the area model papers to help students to conceptualize adding fractions with uncommon denominators. The area model papers we use in the videos (get the free template!) are broken down into 1, 1/2 , 1/4, 1/8, and 1/16. These are friendly fractions to help students understand the patterns of these numbers and how they can add and subtract using different strategies.
This video will show the common types of problems that either have an even answer, or you could offer the opportunity for students to add them and then figure out what the simplest form would be or how to reduce the fraction.
For this example, let’s add 2/4 plus 4/16. First, we’ll build the 2/4 with area model paper, in my case, those are the yellow pieces. Then, add on the 4/16, which in my set are green. With both yellow and green pieces on the whole, then ask the students – how can we add this together??
When we learned how to do fractions (the traditional way), many times our teacher said to skip count and find the least common denominator. But, I want to pose the question: do we really have to find the least common denominator? Could the denominator, in this case, be 4ths? Could the denominator be 8ths? 16ths?
The opportunity for students to look at problems in an inquiry based way, by asking questions and grappling with concepts are what will help them truly learn the concept. Too often, we teach students procedures for concepts they don’t understand. Then, when they get to fractions that have uncommon denominators, they’re automatically programmed to start skip counting by that number and searching for that common denominator.
I n our example, if I were to change the denominator for both fractions to 16, I could take both of my 4ths and put 4/16 on top of each of them. So, 1/4 = 4/16. The other 1/4 would equal 4/16, and then I would have my third set of 4/16. So I would have 12/16 all together.
n our example, if I were to change the denominator for both fractions to 16, I could take both of my 4ths and put 4/16 on top of each of them. So, 1/4 = 4/16. The other 1/4 would equal 4/16, and then I would have my third set of 4/16. So I would have 12/16 all together.
That’s great, the teacher says, but can you reduce that? But what does it mean to reduce or simplify? When we’re asking students to do that, we’re really asking what piece of paper could I lay on top of all 12 of those 16ths to cover it? From there, students can use the papers and see that perhaps we could put 8ths on top of each set of 2/16. One side has 4/8 and the other side of my area model paper has 2/8, which is 6/8. Is that fully reduced? No.
Let’s try 4ths. The 1/4 piece fits over 2/8 , and we can do that 3 times, so the answer is equal to 3/4
Going through this process with concrete manipulatives will help students understand what you mean when you ask them to simplify or reduce the fraction to its simplest form.
If you ask me, 3/4 , 6/8, and 12/16 are all correct answers. You can find arguments that say a fraction has to be in its simplest form to be correct, and other arguments that say it doesn’t matter. I always tell students that, if a question asks you to put a fraction in simplest form, or if you’re looking at a multiple choice and you don’t see the answer you got, to use any equivalent fraction.
Do we necessarily have to teach kids to make all of those 16ths? couldn’t I let the kids think in an inquiry-based way about maybe a more efficient way of answering that? Could I rename my 4/16 as 2/8? Could I rename my 2/4 into 4/8? That’s a possibility because those are all equivalent to the original fractions of 4/16 and 2/4. Of course, then I would add together all of those 8ths and see that I have 6/8, even though it’s not necessarily reduced all the way.
Maybe a student looks at 2/4 plus 4/16 and thinks about adding it as 4ths. Could you rename it the 4/16? Is 4ths the least common denominator? No. So why do we have the rule that students have to skip count to find the least common denominator when in fact, with this example, we’re showing you that it’s actually more work!
In the Classroom
Remember, these videos are great to use as a lesson launch for the instruction you deliver in your classroom. You can use these videos with the flipped classroom concept where students watch the video prior to meeting with you in the Math with the Teacher station. This allows them to bring some background knowledge to the table as you start instruction on the concept.
 Concrete reinforcement in the classroom, after watching the video, is important, and you can use the area model papers, as we do in the video, or you could use pattern blocks, or even patty paper. The whole idea is to help kids understand what’s happening when they’re adding fractions. When students understand the why, the underlying concept, we can teach them shortcuts. Shortcuts in math are great, but shouldn’t be taught unless students really get the concept.
Concrete reinforcement in the classroom, after watching the video, is important, and you can use the area model papers, as we do in the video, or you could use pattern blocks, or even patty paper. The whole idea is to help kids understand what’s happening when they’re adding fractions. When students understand the why, the underlying concept, we can teach them shortcuts. Shortcuts in math are great, but shouldn’t be taught unless students really get the concept.
If you ask me, the “shortcut” of skip counting to find the common denominator isn’t much of a shortcut, especially when I understand equivalent fractions, which makes that process a whole lot easier.
We hope you’ll check out our other YouTube videos in our Working with Fractions series, including multiplying and dividing fractions. Join us next week as we start to look at subtracting fractions!



