Guest Post by Jana Hazekamp, Math Educational Consultant & Coach
Reading strategies in math class? Absolutely!
Many years ago I was considering how I might continue to build my repertoire of strategies for teaching math and helping my students become successful. I was doing a lot of reading about how to teach/guide students to improve their comprehension, and as I read about “reading strategies” I kept thinking…why are we not using these same strategies in math class? Didn’t I want my students to comprehend in mathematics as well? Of course I did! My goal was to develop students who were thinkers, not just answer getters.
So, I asked myself: “What do good readers do? What about good mathematicians?” As I thought, I realized many of the strategies used in each discipline overlapped because they are all about COMPREHENSION!
Let’s compare with a couple of examples:
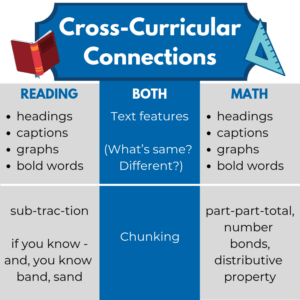 In both reading and math text features are important. We use headings, captions, bold words, pictures, etc. to help us build understanding for a topic. My students dove into informational text by first looking at headings, captions, photographs, bold words, etc. to gain schema before reading.
In both reading and math text features are important. We use headings, captions, bold words, pictures, etc. to help us build understanding for a topic. My students dove into informational text by first looking at headings, captions, photographs, bold words, etc. to gain schema before reading.
When it came to decoding words in reading I was asking kids to “chunk” or decompose words by small parts and then compose them again. In math, we did the same thing with part-part-total, the use of number bonds, and even the distributive property.
My goal was now to help my students know that the strategies we use in one content were equally as useful in other content areas. Metacognition was the key. Some of you may have used this idea from Comprehension Connections by Tanny McGregor.
In reading, I’d taught my kids about what we called “real” reading. Real reading  meant they were not only saying the words of a text but also thinking about what the words said at the same time. They were predicting, making connections, paying attention to text features, asking questions, and monitoring their understanding. “Fake” reading was just saying the words without knowing what had happened. I would never allow my students to read a text and not be able to talk about it in a meaningful way. So, why were students allowed to just give an answer in math and not talk about it?
meant they were not only saying the words of a text but also thinking about what the words said at the same time. They were predicting, making connections, paying attention to text features, asking questions, and monitoring their understanding. “Fake” reading was just saying the words without knowing what had happened. I would never allow my students to read a text and not be able to talk about it in a meaningful way. So, why were students allowed to just give an answer in math and not talk about it?
I challenged my students to apply the same concept to math. Were they doing “real” math or “fake” math? Fake math was just getting an answer. Real math, for our class, became the ability to explain your answers and why you had used a certain strategy, or make connections to other word problems/strategies, etc. So, how do we help our students build comprehension in math class? Let me suggest four big hitter strategies.
- Monitoring Comprehension: In reading students monitor their reading by continually asking themselves questions like, “Do I know what’s happening?” “Can I talk to a friend about my book?” In math, as students are solving word problems or doing computations they should be applying the same principle and asking themselves, “Do I understand what I’m doing?” “Why am I doing it?” “Can I explain what I’m doing to someone else?” We used these “bookmarks” as reminders.
 Making Connections: We were used to thinking about connections in reading by asking how two characters were alike or even how two books were alike. In math, I encouraged my students to find connections between word problems. That meant thinking about how this problem was like another that we had done. Maybe the story had been about students collecting jellybeans and asked the reader to find a missing part. Then, later when we did another story with a missing part, my students could recognize that it was just like the jellybean problem.In reading…How are these characters alike? Different? How are these two books similar? What book/character does this remind you of? Why?
Making Connections: We were used to thinking about connections in reading by asking how two characters were alike or even how two books were alike. In math, I encouraged my students to find connections between word problems. That meant thinking about how this problem was like another that we had done. Maybe the story had been about students collecting jellybeans and asked the reader to find a missing part. Then, later when we did another story with a missing part, my students could recognize that it was just like the jellybean problem.In reading…How are these characters alike? Different? How are these two books similar? What book/character does this remind you of? Why?In math…How are these two word problems similar? Different? How are these solutions similar/different? What word problem does this seem like?
We could also make connections when teaching multiple strategies for different operations. For example we might be solving 9 x 678 using an area model. Then, we might learn how to use the distributive property/model to solve the same expression. We could put both strategies side by side and notice the similarities. Were they really any different? Not really…they were just recorded differently. I want my students to notice and say, “This is just the same thing we were doing yesterday!” Of course I want to prompt them to be able to explain what they mean and practice “real” math and explain what they mean.
- Imagery/Visualization: When reading, my students need to make a movie or get a picture in their mind of what was happening. This should happen in math as well. When reading a word problem, the students should stop and ask themselves what the story is about and take time to get a picture in their mind or even act out what was happening in the story.
 This became a crucial step in our problem solving process. After reading each word problem or math story I had my students stop and think about what the story was about. When students did this they had to “act out” or retell the story without names or numbers to see if they knew the action in the story. For example:24 students are in a classroom. One-fourth of the students have glasses, how many students do not have glasses?Students can pretend there was a group of students who were split into 4 groups and recognize they were looking the number of students who were not wearing glasses. Or they might retell the story by saying something like, “There is a group of students and part of them wear glasses. We need to know how many do not wear glasses.”Visualization is also an important component of computation. Students need to be able to visualize what happens when they’re working with numbers. We can start by using base ten blocks or place value disks to build the problems and help students understand what is going on when we add and when and/or why we regroup, for example. Once they can build problems successfully, students could draw what was happening instead of building it. Finally we can move on to the most abstract level of computation and have students visualize how the manipulatives would move as they record the numbers on paper.This process can apply to more and more complex problems as well. When students look at problems like 5 ÷ ½ or 2 3/4 + 3 ½ they can visualize by asking themselves things like: What is going on? What can I see? Can I draw a picture of what is happening? Can I give it a context
This became a crucial step in our problem solving process. After reading each word problem or math story I had my students stop and think about what the story was about. When students did this they had to “act out” or retell the story without names or numbers to see if they knew the action in the story. For example:24 students are in a classroom. One-fourth of the students have glasses, how many students do not have glasses?Students can pretend there was a group of students who were split into 4 groups and recognize they were looking the number of students who were not wearing glasses. Or they might retell the story by saying something like, “There is a group of students and part of them wear glasses. We need to know how many do not wear glasses.”Visualization is also an important component of computation. Students need to be able to visualize what happens when they’re working with numbers. We can start by using base ten blocks or place value disks to build the problems and help students understand what is going on when we add and when and/or why we regroup, for example. Once they can build problems successfully, students could draw what was happening instead of building it. Finally we can move on to the most abstract level of computation and have students visualize how the manipulatives would move as they record the numbers on paper.This process can apply to more and more complex problems as well. When students look at problems like 5 ÷ ½ or 2 3/4 + 3 ½ they can visualize by asking themselves things like: What is going on? What can I see? Can I draw a picture of what is happening? Can I give it a context - Questioning and Communication: During book clubs in our classrooms students are expected to talk with their teammates about what they are thinking. Did they make a connection to a character, relate to a feeling, or even wonder what or why something happened? Did they talk about what they would have done differently? I want my students talking about books! I feel strongly the same expectations should be there for math as well. Math should not be a spectator sport. Students should be expected to develop language around this discipline, including strategies for questioning. If they are going to question, then we must continually model good questioning. Below is a list of possible question starters you might use and encourage your students to use.

Get your students questioning the who, what, when, where, and why of mathematics! Help them to become not just doers of mathematics but comprehenders.
 Jana has spent more than 30 years being a teacher in various classroom settings – first thru fourth grade self contained classrooms, first-third grade multiage, and K-5 math and reading intervention. Jana is passionate about teaching math for understanding by using manipulatives and drawings (Concrete-Pictorial-Abstract). She is also an advocate for integrating reading strategies into the math classroom in order to develop mathematical thinkers. She has been presenting at the local, state, and national levels for more than 20 years and is the author of Why Before How: Singapore Math Computation Strategies.
Jana has spent more than 30 years being a teacher in various classroom settings – first thru fourth grade self contained classrooms, first-third grade multiage, and K-5 math and reading intervention. Jana is passionate about teaching math for understanding by using manipulatives and drawings (Concrete-Pictorial-Abstract). She is also an advocate for integrating reading strategies into the math classroom in order to develop mathematical thinkers. She has been presenting at the local, state, and national levels for more than 20 years and is the author of Why Before How: Singapore Math Computation Strategies.



