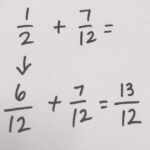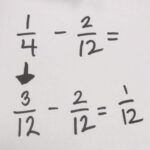Once students have a solid conceptual understanding of equivalent fractions and comparing fractions, the next thing we want to work on is helping kids add and subtract fractions, whether with common or uncommon denominators.
 A common theme in Fraction February is that we don’t want our student to just memorize a procedure in order to get the right answer. For adding and subtracting fractions, we want to steer away from just teaching kids the traditional way of skip counting, finding the least common denominator, switching one fraction and then the other because, even as adults, we don’t completely understand why we do that except that it gives us the right answer.
A common theme in Fraction February is that we don’t want our student to just memorize a procedure in order to get the right answer. For adding and subtracting fractions, we want to steer away from just teaching kids the traditional way of skip counting, finding the least common denominator, switching one fraction and then the other because, even as adults, we don’t completely understand why we do that except that it gives us the right answer.

Prior to adding and subtracting fractions, students needs to have had lots of experiences with the concepts leading up to this point: equal sharing, the whole parts of numbers, building with unit fractions, equivalent fractions, comparing fractions, and then estimating fractions. If kids have a firm grasp of these six components, we can ensure that when they move on to the 7th component, operations (adding/subtracting, multiplying/dividing), they have a repertoire of information that forms a foundation for what they are doing.
Any of the tools that we’ve used previously with estimating or looking at equivalent fractions or comparing fractions will also work with adding and subtracting fractions. The main tools you’ll want to have in your Math Salad Bar are your pattern blocks, patty paper, and area model papers. We also want to bring in lots of work with number lines as well as tape diagrams. For this post, we will continue using the pattern blocks because kids are familiar with this tool, and because, in our previous post, we used the pattern blocks to show equivalent fractions and so the transition to adding fractions using the same manipulatives will be easy for students.
As with finding equivalent fractions, you can represent your whole with just one hexagon, however, this does limit your range of available fractions to halves, thirds, and sixths. So think about changing what the whole looks like as you work with the pattern blocks and, as your students become more comfortable with the concept of adding and subtracting fractions, expand the whole to equal two or more hexagons so you have more flexibility in the types of fractions you work with. However, when you are starting out, you want to pick some friendly fractions to help kids begin to look at adding fractions. Use common fractions or pattern fractions that kids are used to, like halves, fourths, eighths, sixteenths, before you bring in some of the higher level fractions like trying to add halves and ninths.
 Even though we’re moving on to a new concept in the progression of learning to work with fractions, it’s always good to bring in some estimation while we’re adding or subtracting. Get kids thinking about what they know about equivalent fractions and comparing fractions: are these two fractions going to be larger than one? Will the answer be closer to half? Will it be less than half? Will it be closer to two?
Even though we’re moving on to a new concept in the progression of learning to work with fractions, it’s always good to bring in some estimation while we’re adding or subtracting. Get kids thinking about what they know about equivalent fractions and comparing fractions: are these two fractions going to be larger than one? Will the answer be closer to half? Will it be less than half? Will it be closer to two?
Help kids use their knowledge of equivalent fractions to estimate before they add. So, if I was adding 1/2 + 7/12, my thought process might look something like this: “If I have 7/12, I know that it is more than 1/2 because I know that 6/12 is equal to 1/2. I know that 7/12 is more than half, and then they’re asking for another half, so I know that my answer is going to be larger than 1.”
You really want to engage in conversations and talk to students about what they’re noticing as they’re working with fractions. The number talk concept, as outlined in Sherry Parrish’s book Number Talks, is so important to getting kids to think about how would they go about doing a problem instead of just teaching them a formula to memorize.
Let’s look more closely at our sample problem:
1/2 + 7/12

We’ll use 2 hexagons as our whole.
We took 1 hexagon and added in 7 of the triangles which each equals 1/12 and the one hexagon equals one half of our whole (two hexagons).

When kids see problems like this, especially in the abstract, they think they have to approach it in the traditional way. They might write down the problem and start skip counting to look for a way of changing that 1/2. Actually, there are lots of different ways we could add this! One way would be to say I know that I could decompose 7/12 into 6/12 and 1/12. I know that 6/12 plus another half (6/12) equals whole.
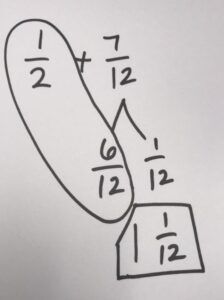
Another way to solve this problem is to take 1/2 + 7/12 and change 1/2 into 6/12 and then add 6/12 + 7/12 to get 13/12. You could even use number bonds to pull out the whole and take the fraction that’s larger than 1 and put it in a mixed number. We have 13/12, pull out 12/12 and 1/12, which gives us 1 and 1/12. The pictures show this model with a conceptual part and the pictorial as well as the abstract. They could actually put the hexagon on top of the 6/12 to see how that would actually represent a whole.
Subtraction is another area where we want to start by using common denominators with the kids so they get the idea of the fractional parts and don’t have to do any renaming of fractions.
In this example, we have two hexagon blocks as our whole, but we are just going to work with ¼. Remember that kids need a lot of reminders about what the shapes represent. As I model this in classrooms, some kids forget and think that the hexagon is a whole. If we’re doing two hexagons, then the trapezoid is a fourth, not a half, so help them remind each other occasionally by saying something like, “Ok, tell your partner what color or what shape is now a fourth if we’re using two hexagons as a whole!”
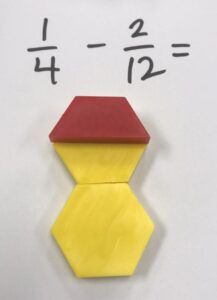
As do this activity in our coaching series with our 4th and 5th grade, it’s done with an inquiry focus. I provide the block and have the students work through the process as I prompt them. I have students build their two hexagons, identify it as the whole, and then show me their ¼ so we can make sure everyone is on the same page. Then, I tell them that, out of their ¼, they owe their friend 2/12.
Sometimes kids look at me a little confused, but if you approach it as an inquiry-based anchor task, it is interesting to see how the kids work through the problem. Some kids say, well, I’m going to change my ¼ into 3/12 to make it so I can subtract, because then I can take away 2/12. Sometimes, some of the kids will just say, “I can’t do that, because I can’t break that trapezoid.” Here, we might have a quick talk about the idea of getting off the escalator, and I ask them, “What do you think you can do?” Some kids might grab different pieces of the pattern blocks to see if they can figure it out using the process of elimination. Sometimes, kids just need a visual to help them see that taking the 1/4 can be broken into 12ths and they can see 1/4 is equivalent to 3/12. A lot of conversations could happen around that by simply asking, “How do you know that 1/4 is equivalent to 3/12 knowing that you know 6/12 is equal to ½?”
Establishing this conceptual understanding for kids is really key in fraction instruction. From this problem, we actually rename 1/4 as 3/12, and from there, its very easy to see how we can take away 2/12 and be left with 1/12.
 This concept could be repeated in many different ways. We could have 1 1/4 – 1/2. You can’t take 1/2 from 1/4, so kids would need to change out the whole fraction into a number that they can regroup or rename so they could actually pull a half away. For this problem, we would need to change the hexagon into 1/4s or 1/2s so we could show how we could take away 1/2 and see what the difference is.
This concept could be repeated in many different ways. We could have 1 1/4 – 1/2. You can’t take 1/2 from 1/4, so kids would need to change out the whole fraction into a number that they can regroup or rename so they could actually pull a half away. For this problem, we would need to change the hexagon into 1/4s or 1/2s so we could show how we could take away 1/2 and see what the difference is.
As you’re doing addition and subtraction, be purposeful to ensure that you’re building conceptual understanding. Get kids to articulate their thinking and engage in conversation about what they’re doing the whole time they’re working with fractions. Eventually, students will move to pencil and paper, but research supports the idea that teaching kids with manipulatives will really help them to be able to see how the patterns emerge, and to really understand what they’re doing with fractions.