There are a variety of manipulatives that can be used for fractions.
When we create our flip book during our 21st Century Math Initiative training for grades 3-5, we look at the main manipulatives that might be used to help students see equivalence and we focus on helping teachers know which manipulative would be the best for kids to use as they’re starting to understand these different concepts.
Top Choices for Fraction Manipulatives
One of my favorite manipulative to use with students is patty paper. Patty paper is just square paper, like the square translucent pieces of wax paper you might see between hamburger patties at the deli. This paper is nice to use while comparing or looking at fractions of different size because you can fold the patty paper or use colored pencils to color different sections of the paper in order to visualize another piece that might be the same size. This manipulative is easily thrown away when you’re done with it, and it’s easy to store in your Math Salad Bar.
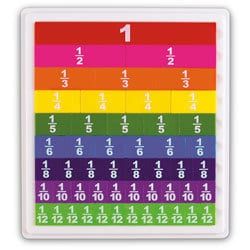Another manipulative that helps kids starting to learn how to compare fractions or even find other equivalents or names for fractions are fraction tiles. These tiles are especially great as a foundational manipulative because they’re labelled, so every tile tells you what fractional part it represents. Sometimes the fraction tiles can be limiting, however, because they do tell which fraction they are, so when you’re renaming fractions with different shapes or different sizes, you are stuck with whatever label it has (1/12 or 1/6) and you can’t change the whole.
Our area model paper was the topic of a Facebook Live video a while back, and it is another great manipulative option. We cut whole sheets of colored paper or cardstock in half, and then in fourths, and then again in eighths, then sixteenths. This is really great for kids to see (as you can see in the video) that, as they lay the papers on top of each other, they can see how those pieces of paper change in size and how they can rename the fractional pieces they are working with.
Pattern Blocks
Today, we’re going to focus on using pattern blocks as a way of showing equivalent fractions, showing different names for fractions, and even being able to compare different fractions. It’s nice to have kids use pattern blocks in a way that lets them explore or come up with different ways to create equivalent fractions. Sometimes, we think that pattern blocks could be limiting because we might only see the traditional construction of a hexagon as the whole, a trapezoid as a half, a rhombus as a third, and then a triangle as a sixth. But we want to be able to use these blocks to help kids create different fractional parts. We can think outside the box and we might change our whole to be two hexagons or even three hexagons. If we do this, we can create larger groups of pieces and maybe the trapezoids could actually represent the fourths, the rhombuses represent the sixths, and you could have the twelfths represented by the triangles.
During one of our trainings this week, we were working with one of our teachers and had three hexagons as our whole. We were able to go all the way up to eighteenths with the triangles, the trapezoids were the sixths, and the rhombuses were ninths. This configuration gave a large variety of blocks to able to show things in different ways. Sometimes, when they’re playing with pattern blocks, kids want to take the whole and match up the perfect shape, but we want them to be able to play and come up with different ways to show, for example, something that might be equivalent to 1/2.
The point of doing this is to help kids develop conceptual thinking around fractions. Often, fractions are a very abstract concept for kids that they can’t quite visualize. Because most students start using pattern blocks at a young age, we can take a simple manipulative and ramp it up to fit our purposes. We can use pattern blocks not only with equivalent fractions or renaming or comparing fractions, but we can also use them for addition, subtraction, multiplication and division, as you’ll see in the rest of our fraction series (stay tuned for more)!
Fraction Equivalence with Pattern Blocks
Let’s do some examples! Let’s start with two hexagons as the whole and you can see all the different options that a child might come up with to see that the half can be renamed lots of different things based on the fractional part. We have the option of doing a fourth, a sixth and a twelfth, which provides more ways of showing equivalence. Sometimes kids have a hard time transferring just from the hexagon being the whole and they have a hard time renaming all the parts. In this case, kids will come up with the obvious fractions such as 1/2 = 2/4 = 3/6 = 6/12. This pictures shows the equivalents to half:
You can also use this exercise to talk about benchmark fractions. Kids should be able to automatically identify what they know about these fractions when they see them – 2/4, 3/6, 5/10, 6/12 – they’re all equal to half!
Part of the exercise is to see if kids can come up with different ways that things can also equal half. Ask them if 1/4 + 1/6 + 1/12 = 1/2. They’ll probably say no! When they’re looking at fractions, they’re often very confused about what the denominator means as well as the significance of a common numerator, and so they have a hard time identifying what size piece we’re talking about. This picture maps out different options to help kids see equivalence. One half could be 1/6 + 4/12 or it could equal 1/4 + 3/12, or any of the other options. The idea here is to get kids to constantly rename pieces:
Let’s do this exercise having three hexagons as my whole. We’ll call it a snowman!
We might pose the question to our students: How many ways could we rename 2/3? Or how many ways could rename any fractional part that is involved in this shape? In this case, with using the three pieces of the pattern blocks, we know that each hexagon is worth 1/3, the trapezoid is going to equal 1/6, the rhombus is going to equal 1/9, and the triangles equalling 1/18. You can ramp up with kids showing different equivalence, start to get them to understand how to compare fractions, and then to be able to put fractions in order smallest to largest.
Ordering Fractions
In this picture, we’re going to use three hexagons as the whole and we’re going to compare the three fractions – 3/9, 3/6, 8/18. Kids typically look at the denominators to figure out how many pieces something is divided into. But when they see the denominator is larger, they feel that that piece is bigger because the actual number is bigger. Sometimes we also have to look at the top number to employ the concept of a common numerator. Looking at 3/6 and 3/9, I know that ninths are divided into more pieces than sixths, and they have a common numerator of 3. We want kids to reason, or estimate, which fraction is larger. So, if we were to think about eating 3 slices of a pie cut into 9 pieces or eating 3 slices out of a pie cut into 6 pieces, we would probably realize which one is larger. Kids might look at the 3/6 and also realize that it’s equal to 1/2 . 8/18 can be tricky because the denominator is larger, but the numerator is 8, so it’s bigger than the 3s we had in 3/6 and 3/9. Let’s see how this looks:
Most of the time, 8/18 is ordered as the smallest because the denominator has the largest number in it. However, kids start to understand that, when fractional pieces break up, that might be the least amount of pieces. Then they’ll think about 3/9, and then 3/6. But often it’s not until you look at the fractions like you see them in the picture that you can actually have the visualization to understand what fractional parts mean.
Establishing Conceptual Understanding
The key component as we start Fraction February, for kids in 4th, 5th, and even 6th grade, is establishing conceptual understanding. Kids don’t have this for fractions because they’re trying to memorize concepts with procedures they don’t really understand. Helping students understand this pivotal piece will lead them to a conceptual understanding that will serve as the foundation for addition, subtraction, multiplication and division, as well as whole numbers later on.
