In the 21st century, motor skills aren’t always as developed as they should be before kids enter kindergarten.
 A child’s life today typically involves more time being plugged in than being outside playing – jump-roping, hopscotch, kick the can, etc. Kids are learning to ride bikes much later and many still struggle to tie their shoes.
A child’s life today typically involves more time being plugged in than being outside playing – jump-roping, hopscotch, kick the can, etc. Kids are learning to ride bikes much later and many still struggle to tie their shoes.
You might be asking yourself does motor really matter for academic achievement? The answer is a resounding YES!
Motor development, such as skipping, crossing midline, rhythmic repetition of clapping in a series or using your body in a pattern, is connected to the beginning of mathematical foundations for students. Just like dynamic and static balance are readiness skills that indicate a readiness for reading, so skipping or crossing midline is indicative of readiness for math.
Unfortunately, there is often a misunderstanding around the term readiness. Readiness is not a guarantee, it simply means that the skills required to get to the next level have been built previously. It doesn’t mean that, if your child can skip, they’re going to be a math genius. It doesn’t mean that if a child can balance on one foot with their eyes closed, that they’ll be a super reader.
Download our free screener and activities here!
A Tale of Two Students
I was working in a kindergarten classroom earlier this fall in one of our project schools. This school is on their second year in our M³ program and they are focusing on the area of problem solving with story problems. It was early in the school year – this school starts towards the end of August and I was visiting towards the end of September – and while I was modeling in the kindergarten classroom, I was able to spend some time observing the students as they responded to different things.
Some of the things I observed had me curious about the way several of the students were processing. Since I was scheduled to be meeting with the new math interventionist after I left that classroom, I thought it was a great opportunity to see if my intuition was correct based on my observations. We pulled a few students to take with us, and my plan was to model the numeracy screeners for the interventionist.
In the video, you’ll see two girls – “Allison” has a unicorn on her shirt and “Jordan” is wearing light blue pants with sparkly accents. I didn’t pull these girls because I thought they were necessarily more at-risk than the others, but the things they were doing during my math lesson piqued my interest about their mathematical thinking.
To begin, I wanted to see if they could just cross their midline. I had Allison and Jordan stand side-by-side and asked them to watch me as I demonstrated a cross crawl and crossed my midline. I didn’t want it to be difficult for them, so I had them just tap their knee with the opposite hand and then alternate.

In this video, you can see that the two students are doing it quite differently. Jordan was very rhythmic – she’s hitting her right hand with her left knee and then fluidly switching to the other side. Allison is really struggling and she spent the whole time watching Jordan to see if she could figure out how she was doing that.
I asked the interventionist if she could predict how well the girls would do on the numeracy screener based on how they were doing with crossing their midline.
As we know, math goes beyond just knowing numbers, and so my question was really whether or not these students would have kinesthetic one-to-one correspondence. My prediction was that Jordan, the student who could cross her midline, would do well on the kinesthetic one-to-one correspondence, but that Allison, the student who was struggling and more motorly awkward, would reveal this to be an underdeveloped area for her.
Why is crossing midline so important for both reading and math?
 I remember doing a Finger Funatics training early on, not too long after I’d published the book. I did a lot of preK trainings and after one of them, a mother came up to me and asked me to watch her son Joey as he wrote his name. Little Joey was very confident in his abilities, and I handed him paper and a pencil right at his midline so I could see what he would do.
I remember doing a Finger Funatics training early on, not too long after I’d published the book. I did a lot of preK trainings and after one of them, a mother came up to me and asked me to watch her son Joey as he wrote his name. Little Joey was very confident in his abilities, and I handed him paper and a pencil right at his midline so I could see what he would do.
Joey picked up the pencil with his left hand, and in the left corner of the paper that lined up with his body, he wrote the letters J and O. As the word was going to “cross the midline” of the paper, Joey put down the pencil, picked it up in his right hand and finished writing the E and Y. It was baffling!
From there, I had Joey do some of the same kinds of exercises we do in our Finger Funatics. Could he do a cross crawl and cross his midline? The gym we were in had patterns made of painted cinderblocks on the wall – could Joey trace the pattern, but face forward and cross his arm completely across his body to make a T? Interestingly, Joey took his left hand, traced the line on the wall until it got to his midline, and then used his right hand to resume and finish tracing.
Clearly, Joey was struggling to cross his midline, but at four years old, Joey’s mother wasn’t sure why that mattered. Think about a child’s school day – so often the right side of the brain has to talk to the left, the front has to talk to the back. How often does the child need to have all the parts of their brain working at one time? Very frequently! If the child’s extremities can’t cross their midline, any processing that requires the brain to “cross the midline” will be weak.
Because of this, we give parents a lot of different activities they can do at home to help their kids cross the midline, which will in turn help them academically.
Administering the Numeracy Screener
 Download our free screener and activities here!
Download our free screener and activities here!
After we made our predictions about Allison and Jordan’s performance on the kinesthetic one-to-one correspondence screener, I then had them count to ten for me. Counting to ten by rote is a prerequisite for the kinesthetic portion of the numeracy screener. Both of the girls could indeed count to ten, so they had the necessary skills to begin administering the numeracy screener!
In preparation for the screener, we laid out poly spots in numerical order from one to ten. Each was marked with a dot pattern, and we had also marked a starting line just before the first poly spot. This line is a good idea so that, as kids start to walk on the stepping stones of the poly spots, they can begin counting with their first step.
When we’re doing the screener, I’m not trying to trick the students as they’re walking on the poly spots. In fact, with these girls in this video, I held their hands and showed them how I wanted them to walk on the number line. I said, “If I ask you to walk five steps forward, I’m going to count out loud and walk my steps, like this – one, two, three, four, five.” It’s important to the assessment that they understand this concept. If they know how to do it, they’ll do great, if they don’t, they won’t.
I relate kinesthetic one-to-one correspondence with rhyming. You can’t really make a kid have kinesthetic one-to-one correspondence any more than you can make a kid rhyme. Imagine pulling a child off to the side and asking them to supply you with two rhymes based on the rhymes you give them. You say cat and hat and they give you a blank stare and say water bottle. You try again. You say chair and bear and they say pencil. The child might be naming things they see, maybe not even knowing what a rhyme is. In rhyming, we do a lot of different kinds of songs and games and rhythmic activities to help students to hear the rhyme, but at the end of the day, even if we beat our head against the wall, the child has to hear the rhyme on their own. It’s the same with kinesthetic one-to-one correspondence.
 We had Jordan start at the tape line and walk on the number line, counting as she went. I was watching to make sure that her feet and her body movement were corresponding with the way she was counting. Although she is walking a little bit robotic, she is spot on in counting in succession. We felt like Jordan was confidently ready to move on to our number quantity screener.
We had Jordan start at the tape line and walk on the number line, counting as she went. I was watching to make sure that her feet and her body movement were corresponding with the way she was counting. Although she is walking a little bit robotic, she is spot on in counting in succession. We felt like Jordan was confidently ready to move on to our number quantity screener.
It is important to have kids repeat the exercise a few times – not just go to the number four and come back. We want to then have them come back and walk to the six and then come back, walk to the five and come back, walk up to the eight and come back. Some students that might be cognitively impaired or seriously at-risk can only count to the number five. They will be able to do the numbers one through five consistently, but then as soon as they go to six there is confusion, so sometimes we’ll work on kinesthetic one-to-one correspondence by taking off the six, seven, eight, nine and ten.

You can see how Allison, even as she is waiting to go on the number line, is almost losing her balance and seems to be motorly awkward. She’s very impulsive when she’s doing things, and as she walks on the number line, she struggles with one-to-one. At one point during the video, she looks like she has it pretty consistently, but I’m not convinced. I have her try it again and come back, and again and come back. If it’s not demonstrated consistently, just like if the child were to be rhyming and they said cat, hat, fat, and then all of a sudden they said lick, you’d know that pattern wasn’t really sticking.
It was very evident that Allison was really struggling with kinesthetic one-to-one correspondence. Even if I got her to slow down, she still couldn’t connect her kinesthetic walking with a number in a rhythmic way to have what we call kinesthetic one-to-one correspondence on a destination. For her, the appropriate level might be to work on numbers one through five to help her keep consistent and then start to build the numbers in the poly spots.
The Next Level
 The next part of the assessment is to remove the poly spots and have them walk to me from a certain location in the classroom, counting as they walk. In this particular classroom, this interventionist, as with all interventionists, ended up with lots of different things in her classroom, including a Christmas tree. The girls stood by the Christmas tree and then I wanted them to walk over to me by the teacher’s computer. Again, I wasn’t trying to trick them. I demonstrated so they could see that I was walking, and each step that I took was one-to-one corresponding to the number I was saying in succession.
The next part of the assessment is to remove the poly spots and have them walk to me from a certain location in the classroom, counting as they walk. In this particular classroom, this interventionist, as with all interventionists, ended up with lots of different things in her classroom, including a Christmas tree. The girls stood by the Christmas tree and then I wanted them to walk over to me by the teacher’s computer. Again, I wasn’t trying to trick them. I demonstrated so they could see that I was walking, and each step that I took was one-to-one corresponding to the number I was saying in succession.

My prediction was that Jordan, since she was able to walk on the poly spots, would still have kinesthetic one-to-one correspondence if they were removed. As you can see in this video, she does a great job with it.
With Allison, my prediction was that if she couldn’t do one-to-one correspondence on a destination, she would still not have it without the poly spots to walk on. We had to do two different takes with her because she was so impulsive and walking so fast. Even when she went slower, as she got going, she ended up losing it.
Why is this really important?
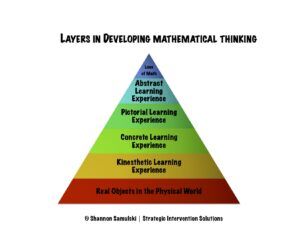 In the developmental pyramid, the student’s first exploration of math is with real objects in the physical world and then they develop this kinesthetic world before they start to understand or conceptualize math with Concrete Pictorial Abstract. This kinesthetic aspect is really important in lots of concepts in math, not just in the kinesthetic one-to-one correspondence. Think about kids learning to do multiplication for the first time. They might act it out, look at it in groups, or on an open number line showing shifts in the number line. Any time you can bring a math concept down to the kinesthetic level, you are helping solidify the foundation of that skill, almost like a layer before the concrete level.
In the developmental pyramid, the student’s first exploration of math is with real objects in the physical world and then they develop this kinesthetic world before they start to understand or conceptualize math with Concrete Pictorial Abstract. This kinesthetic aspect is really important in lots of concepts in math, not just in the kinesthetic one-to-one correspondence. Think about kids learning to do multiplication for the first time. They might act it out, look at it in groups, or on an open number line showing shifts in the number line. Any time you can bring a math concept down to the kinesthetic level, you are helping solidify the foundation of that skill, almost like a layer before the concrete level.
Many of the students that don’t have kinesthetic one-to-one correspondence, typically don’t have kinesthetic one-to-one correspondence with objects either. You can see this if you sit with a student and count one, two, three, four and move the counters as you count, but when it’s thier turn, they start moving the counters faster than they’re counting and their words and actions don’t line up. And so, that’s usually an indicator that they don’t have the kinesthetic one-to-one. As we’ve learned from this experience, these students might be motorly awkward or haven’t mastered crossing their midline.
What do we do next?
I’m not sure if this is sad news or good news, but if this layer of kinesthetic correspondence goes underdeveloped and we ignore it in schools, if we crack open that kindergarten book and start to plow through it, they won’t have the readiness they need to go into mathematics. And in an at-risk school district, it is probably not just one or two, but ten or fifteen students that don’t have the rhythmic pieces of math. Learning kinesthetic one-to-one correspondence is pivotal and it’s not hard either!
For kids that need to work on this area, we usually have them doing an intervention group, which is what the interventionist was planning to do with Allison and Jordan. If Allison were to be pulled out ten minutes a day, every day for three weeks, that would give her a little less than an hour a week, about three hours of time, on an exact instructional match which is helping her build kinesthetic one-to-one. Nine times out of ten, that’s all it takes for the kids to develop that layer of learning because it’s something that’s been underexposed and they just haven’t yet developed it.
Some ideas for developing kinesthetic one-to-one correspondence

It’s all about finding a way to integrate it into our environments so that kids can really use the skill and make sure they’re really understanding.
Download our free screener and activities here!
- Walk around the school and count steps. For example, as they walk out to recess, have them count their steps on the black top before they get to the playground or put a large lazy eight on the floor in the hallway and having kids walk it and count their steps around it.
- Rhythmic body movements. I might tap right, left, left and I might have the child tap on their knee. Or I might do head, shoulders, tummy, and then repeat.
- Bean bags. Tossing a bean bag into a target and counting. Or tossing the bean bags to the student and telling them to stop when they have five.



