Teacher's Guide
Episodes 305-306
February Focus: Word Problems
In these warm-ups, we’ll use a step-by-step visual model process, which will vary slightly depending on the grade level and what type of problem that we’re working on. Professor Barble helps students slow down, think about what the word problem is asking, and organize the information it conatins before they jump right into solving it. Yes, we even do this in Kindergarten! See sections below for more specific information about how word problems and model drawings are used in each grade.
Kindergarten

Focus: 305: Break Apart Pattern Block Designs/ 306: Compose and Decompose Numbers to 9
“I Can” statement: I can compose and decompose numbers to nine. / I can compose and decompose numbers up to nine with towers.
Extension Activity: Matching Expressions / Two Parts to Make Seven
In the Kindergarten 305 episode, we’re going to continue with word problems with Professor Barble. This time we look at some different types of problems, still not going higher than sums of 10. For example, John has a paperclip chain. He has five large paper clips and puts on three small paper clips, how many paper clips does he have? Students are modeling this out with the Math Work Mat, showing that organized quick draw, modeling in the 10 frame, a number bond, and then filling in the computation statement to match. The “I Can” statement is: I can compose and decompose numbers to nine.
 We invite students to the lesson by having them look at different pattern blocks, orange squares and purple diamonds. There are four combinations labelled A, B, C and D, and we want to see what things kids notice about which one wouldn’t belong.
We invite students to the lesson by having them look at different pattern blocks, orange squares and purple diamonds. There are four combinations labelled A, B, C and D, and we want to see what things kids notice about which one wouldn’t belong.
In Kindergarten, we typically only have one thing that doesn’t belong, but this show stretches kids’ thinking a little bit to see if they can find reasons to argue that each one of the choices doesn’t belong in some way. One student might say one of them has seven shapes and the rest have six shapes, so that one doesn’t belong. Someone else might say that one of them doesn’t have any squares, and it doesn’t belong because it’s all diamonds. We want kids to pay attention to the part and the part and the total, or the way things are organized, but this concept will also allow all students to contribute to the lesson in some way.
We do a fun activity with pattern blocks to see if students can create something with only seven pattern blocks in a combination of green triangles and orange squares. We can create a house or we might create a castle, and we can use our creation to relate to the sums of numbers. I used three triangles and four squares to create my house, which total seven pattern blocks. In your castle, you used two triangles for the peak and five squares for the base. It’s all about approaching things in different ways, being given a quantity and seeing the part-part-total.
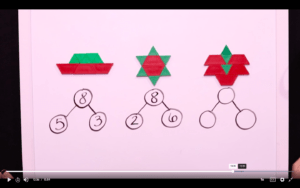 We continue this by looking at combining trapezoids and triangles and using a total of eight pattern blocks to see what we can make. Someone creates a boat, one student creates a star, and we also have a rocket. If we wrote the statement 5 + 3, is that true of all three of these pictures? Here, we want to get Kindergarteners to see that their opinion matters and that they can apply their thought process. They might disagree with that statement, and so then we go through and figure out which one of the designs doesn’t match.
We continue this by looking at combining trapezoids and triangles and using a total of eight pattern blocks to see what we can make. Someone creates a boat, one student creates a star, and we also have a rocket. If we wrote the statement 5 + 3, is that true of all three of these pictures? Here, we want to get Kindergarteners to see that their opinion matters and that they can apply their thought process. They might disagree with that statement, and so then we go through and figure out which one of the designs doesn’t match.
For the extension activity, kids see a set of pattern block designs and have to determine which expression goes with which design, based on the part-part-total composition of the design. This is a fun way for kids to engage in this concept with a different type of manipulative – We don’t have to always use unifix cubes for kids to get that idea of part-part-total!
 In show 306, we continue with word problems and helping students to do adding with two different numbers. Hopefully, by now, students are becoming a bit more fluid with this problem solving process that we have outlined in the Kindergarten Journal, as we’ve focused on it quite a bit in the shows this month. With continued practice, problem solving should be becoming easier and more natural for Kindergarteners.
In show 306, we continue with word problems and helping students to do adding with two different numbers. Hopefully, by now, students are becoming a bit more fluid with this problem solving process that we have outlined in the Kindergarten Journal, as we’ve focused on it quite a bit in the shows this month. With continued practice, problem solving should be becoming easier and more natural for Kindergarteners.
Our objective here is very similar to the previous show: I can compose and decompose numbers up to nine with towers. As you know, we can’t give students enough practice with this concept. Whether we do pattern blocks or we use the counting buddy or we use towers, kids need repetition with this concept of decomposing and composing numbers.
To invite kids into this lesson, we lay out different trains of unifix cubes and ask students what they notice and what they wonder. What’s the same? What’s different? All of the trains total six, as students will discover, but we have one broken into three and three, one broken into four and two, and one broken into one and five.
D.C. definitely appears in this show! Even though Kindergarteners aren’t necessarily using D.C. to decompose and make a 10, they’re still learning to break apart cubes, which is the premise of our game called Snap the Cubes. D.C. has a row of nine cubes, and he uses his hammer to smash it. Player One decomposes the cubes in a certain way. Player Two has to describe how the cubes are broken up. There’s a nice recording sheet that helps students create different combinations as they’re breaking the cubes apart to see the expressions that match.
 Through this activity, we hope that kids will see the pattern that emerges if I do one and eight, and then two and seven, and then three and six, etc. If we were adding to eight, it could be two and six, three and five, four and four, etc. As they build with the unifix cubes and record their combinations, they’ll be able to see the progression of the two parts.
Through this activity, we hope that kids will see the pattern that emerges if I do one and eight, and then two and seven, and then three and six, etc. If we were adding to eight, it could be two and six, three and five, four and four, etc. As they build with the unifix cubes and record their combinations, they’ll be able to see the progression of the two parts.
And so as the extension activity, kids play Two Parts to Make Seven. Given a set of seven unifix cubes in a drawing, kids get to select which two parts they’re going to color in and create that expression. Ultimately, we want kids to be really flexible in their understanding for these concepts so that they’re able to apply them as they’re starting to learn more about part-part-total.
First Grade

Focus: 305: Add 2-Digit Numbers & Write Equations / 306: Decompose/Compose to Add
“I Can” statement: I can add numbers, and write equations to show my work. / I can add two-digit numbers to a one-digit number by decomposing and composing.
Extension Activity: Adding with Value Pak / Solving with D.C.
 In show 305, we’re continuing to work with Professor Barble at the beginning, this time using a non-proportional approach for part-whole addition. Our journal page is similar to what we’ve used in the past, but instead of the unit bar being labelled with individual units, it’s open. Kids have to figure out where to put the marks to represent quantities in the problem. If someone has six green apples and three red apples, I’m not going to put that line directly in the middle of the bar, because six doesn’t represent an equal half of the total. Instead, I’m going to move it over a bit to the right because six is larger than three. This warmup problem gets kids to start to understand the idea of proportioning a bar out, and so we go through the whole step-by-step process just a little bit differently.
In show 305, we’re continuing to work with Professor Barble at the beginning, this time using a non-proportional approach for part-whole addition. Our journal page is similar to what we’ve used in the past, but instead of the unit bar being labelled with individual units, it’s open. Kids have to figure out where to put the marks to represent quantities in the problem. If someone has six green apples and three red apples, I’m not going to put that line directly in the middle of the bar, because six doesn’t represent an equal half of the total. Instead, I’m going to move it over a bit to the right because six is larger than three. This warmup problem gets kids to start to understand the idea of proportioning a bar out, and so we go through the whole step-by-step process just a little bit differently.
A lot of first grade teachers want to continue putting that individual unit into the drawing. However, soon, someone’s going to have 16 apples and 12 apples, and that’s going to be too many individual units to write in. So, at that first grade level, we really encourage students to make the unit bar match what they’re using by writing in their own unit quantities.
 The I Can statement is: I can add numbers, and write equations to show my work. And so we have Molly and Han, who are trying to find the sum of 24 + 63. Molly starts off with 20 plus 60. Can we figure out what her next step should be? Students are going to solve these problems in different ways. In this case, Molly is solving with Value Pak, adding the 10s first and then she will need to do the ones. Han takes a different approach for 24 + 63. Han decides to start with 63 and then add 20 to get a total of 83. What does he have to do next? This strategy shows a different approach. Han is taking the whole number 63 and then just adding in the 10s, so eventually he has to do the ones as well. Obviously, we want students to be able to create the methods and the equations that are easiest for them, but we also want them to distinguish how students are adding in different ways. We have students try to match the expression they see to which expressions you might use to find the sum.
The I Can statement is: I can add numbers, and write equations to show my work. And so we have Molly and Han, who are trying to find the sum of 24 + 63. Molly starts off with 20 plus 60. Can we figure out what her next step should be? Students are going to solve these problems in different ways. In this case, Molly is solving with Value Pak, adding the 10s first and then she will need to do the ones. Han takes a different approach for 24 + 63. Han decides to start with 63 and then add 20 to get a total of 83. What does he have to do next? This strategy shows a different approach. Han is taking the whole number 63 and then just adding in the 10s, so eventually he has to do the ones as well. Obviously, we want students to be able to create the methods and the equations that are easiest for them, but we also want them to distinguish how students are adding in different ways. We have students try to match the expression they see to which expressions you might use to find the sum.
 Another example would be 24 + 32. We show six different expressions and students have to determine, could you use this? Well, obviously someone could do 30 + 20, and then 4 + 2. Somebody else could have taken 32 and then added 20 and then added four. This is a bit of a harder task, but helps students become a bit more analytical, as they have to look at the six expressions and decide which two were used to solve the problem.
Another example would be 24 + 32. We show six different expressions and students have to determine, could you use this? Well, obviously someone could do 30 + 20, and then 4 + 2. Somebody else could have taken 32 and then added 20 and then added four. This is a bit of a harder task, but helps students become a bit more analytical, as they have to look at the six expressions and decide which two were used to solve the problem.
And so students get to solve with Value Pack for two digit plus two digit numbers. Now again, students can decompose and solve by adding 10s and 10s and then ones and ones, But they also could take the larger number, and then count up if they chose.
As we move on to show 306, students are again working with Professor Barble. This time, we are solving a part-whole missing addend with a non-proportional bar. We have students label the total with a part that has a quantity and a part that doesn’t, it’s unknown. There were 12 coats on a rack. Seven of them were pink, the rest were blue. How many blue coats were there?
 The important thing is to make sure students get really good at labelling what they’re adding to their drawing. Pay close attention to how Mrs. Markavich labels what each quantity means so she can go back and chunk and check those parts of the problem as she’s adding it.
The important thing is to make sure students get really good at labelling what they’re adding to their drawing. Pay close attention to how Mrs. Markavich labels what each quantity means so she can go back and chunk and check those parts of the problem as she’s adding it.
The I Can statement is: I can add two-digit numbers to a one-digit number by decomposing and composing. The introductory part of this is similar to a previous number talk where we ask kids to look at how many they see and add on more. So we see three 10-frames filled and then we add on some more. How can students look at the groupings of 10 and quickly determine the quantity without counting? This takes the idea of a numeracy talk a little bit further.
Then, we ask what might be the most efficient way to add if we have a problem like 8 + 47. One student decides to put 47 in their head, and do +1, +1, +1, 48, 49, 50, 51, etc. That works, but for first graders, is that the most efficient strategy?? Maybe not. Maybe we should use D.C.! D.C. has a big part of this show to help students understand how to decompose to create that new 10. So if I’m doing 8+ 47, I might want that 47 to become a 50. I’m going to decompose 8 into 5 + 3, and make that next decade number.
 Don’t forget that students really need visual assistance for this! On the show, I have a mat with six 10-frames on one big sheet (you could print it on legal paper and have kids fill it in). You could also use an abacus to help them see how to decompose numbers in order to add.
Don’t forget that students really need visual assistance for this! On the show, I have a mat with six 10-frames on one big sheet (you could print it on legal paper and have kids fill it in). You could also use an abacus to help them see how to decompose numbers in order to add.
I really like the extension activity here because it’s Solving with D.C. For each problem, students have five empty 10 frames because I really want students to be able to build the first number on the 10 frames, and then start a fresh 10 frame to build the second number so they can see how to decompose to make that decade number.
Second Grade

Focus: 305: Compare 3-Digit Numbers: Part 2 / 306: Order 3-Digit Numbers
“I Can” statement: I can use place value to compare 3-digit numbers. / I can order three-digit numbers using place value understanding.
Extension Activity: Make the Greater Number / Help Value Pak Get In Order
 In episode 305, we are using Professor Barble, but we’re actually doing a full problem with him! I chose to do additive comparisons here because I think that second graders really struggle with this concept. It’s harder than the more simplistic part-whole addition, part-whole subtraction, or part-whole missing addend kinds of problem. Doing an additive comparison helps students learn to put in a value for each person as they’re creating their visual model. For example, Mallory has 36 crayons and Nolan has 4 more crayons than Mallory. How many crayons does Nolan have? Oftentimes, kids are taught to circle the numbers and underline the important words, so most kids would come up with 36 + 4 = 40. However, we want kids to have more of a sense of what the words are asking by putting in a unit bar for each character and then adding in and adding the values. You’ll see how it makes this kind of problem a lot easier for kids to solve.
In episode 305, we are using Professor Barble, but we’re actually doing a full problem with him! I chose to do additive comparisons here because I think that second graders really struggle with this concept. It’s harder than the more simplistic part-whole addition, part-whole subtraction, or part-whole missing addend kinds of problem. Doing an additive comparison helps students learn to put in a value for each person as they’re creating their visual model. For example, Mallory has 36 crayons and Nolan has 4 more crayons than Mallory. How many crayons does Nolan have? Oftentimes, kids are taught to circle the numbers and underline the important words, so most kids would come up with 36 + 4 = 40. However, we want kids to have more of a sense of what the words are asking by putting in a unit bar for each character and then adding in and adding the values. You’ll see how it makes this kind of problem a lot easier for kids to solve.
As we move on, we continue with place value and looking at using three-digit numbers to compare. We play a fun game where students get to decide if the statement is true or false. The catch is that the statements are not just going to be two different numbers, but they involve addition! For example, 330 < 300 + 3. Kids are required to solve the addition problem before they decide if the statement is true or false. For the example, kids have to be careful to attend to place value in order to see that the statement is false.
 In previous shows, we’ve talked about all these different ways to compare. In this show, students have to decide which one they want to use. If you had 521, and you were going to compare it to 523, would you use Value Pak and build it looking at the hundreds, 10s and ones? Would you use base-10 blocks like we have in the past? Would you use discs? Or would you use the number line? Students can pick a strategy that best works for them! One student might find the place value discs are easier to use, where another student might find using the number line is easier. We want kids to have this freedom!
In previous shows, we’ve talked about all these different ways to compare. In this show, students have to decide which one they want to use. If you had 521, and you were going to compare it to 523, would you use Value Pak and build it looking at the hundreds, 10s and ones? Would you use base-10 blocks like we have in the past? Would you use discs? Or would you use the number line? Students can pick a strategy that best works for them! One student might find the place value discs are easier to use, where another student might find using the number line is easier. We want kids to have this freedom!
The last activity in this show is giving kids three numbers that could potentially fit into a statement more than once. They have to figure out which numbers go into which statements. And so we have different blanks for greater than or less than, and kids kind of have to use their thinking caps a little bit here to figure out which number will fit into which statement.
For the extension activities, we have Make the Greater Number. In this game, kids will spin the wheel and combine digits to apply the ideas we’ve been talking about with place value and make a greater number than their partner.
 As we move on to 306, we’re going to continue with the Professor Barble warm-up, and I do another additive comparison problem. I really want kids to slow down to read the problem! Diego read 15 more pages than Jaida. Well, if we don’t have that unit bar for each student, that could be a really difficult problem to solve!
As we move on to 306, we’re going to continue with the Professor Barble warm-up, and I do another additive comparison problem. I really want kids to slow down to read the problem! Diego read 15 more pages than Jaida. Well, if we don’t have that unit bar for each student, that could be a really difficult problem to solve!
The I Can statement is: I can order three-digit numbers using place value understanding. Up to this point, we’ve done a lot with greater than, less than, and equal to, but can students now put them in order?
I love the idea of posing a problem that might be incorrect and having students become detectives, instead of having the teacher always being the person that’s telling them right from wrong. In this show, we have a list of numbers that Kiran and Andre order from smallest to largest and they have to decide if they think that both students’ orders are correct. We get different feedback – someone uses a number line to tell why a number isn’t in order, somebody else uses the Value Pak to get the idea.
 There’s a valuable realization for students here as to the efficiency of strategies. If I give you five numbers ranging from 700 to 850 and asked you to put them in order from least to greatest, and you started using a number line to plot them, the work is already done for you because it’s in order from least to greatest! Another student might start ordering by place value and start with all the numbers in the 700s, then move to the 10s, then the ones, then go back to the numbers that are in the 800s, then look at the 10s and the ones, and then finally plotting the numbers. That takes time. Maybe another student prefers base-10 blocks. Well, gosh, that would take kind of a while to build five different numbers with base-10 blocks in order to compare. Is it easier for us to look at the digits like Value Pak? Or is it easier to look at the number line? Again, the idea we want to communicate is that there can be more than one way and that my way doesn’t have to be the same as my partner’s.
There’s a valuable realization for students here as to the efficiency of strategies. If I give you five numbers ranging from 700 to 850 and asked you to put them in order from least to greatest, and you started using a number line to plot them, the work is already done for you because it’s in order from least to greatest! Another student might start ordering by place value and start with all the numbers in the 700s, then move to the 10s, then the ones, then go back to the numbers that are in the 800s, then look at the 10s and the ones, and then finally plotting the numbers. That takes time. Maybe another student prefers base-10 blocks. Well, gosh, that would take kind of a while to build five different numbers with base-10 blocks in order to compare. Is it easier for us to look at the digits like Value Pak? Or is it easier to look at the number line? Again, the idea we want to communicate is that there can be more than one way and that my way doesn’t have to be the same as my partner’s.
In our extension activity, Value Pak needs some help! They’re all mixed up, and students have to help get them into the right order again.
Third Grade

Focus: 305: Representing Division: Part 2 / 306: Dividing with Even Larger Numbers
“I Can” statement: I can divide using the multiplying up strategy. / I can divide within 100 where the quotient, and the divisor is more than 20.
Extension Activity: Divide with Mutliplying Up / Compare and Estimate Quotients
 In Episode 305, we continue with Professor Barble, now actually doing a word problem with multiplication. We want kids to understand how we can divide the bar into equal sections to represent groups – for example, there were five crates of milk with nine milk cartons in each, how many milk cartons are there in all? Having students draw a visual model to make sure they understand this concept is really important.
In Episode 305, we continue with Professor Barble, now actually doing a word problem with multiplication. We want kids to understand how we can divide the bar into equal sections to represent groups – for example, there were five crates of milk with nine milk cartons in each, how many milk cartons are there in all? Having students draw a visual model to make sure they understand this concept is really important.
We spend a little bit more time on this with the I Can statement of “I can divide using the multiplying up strategy.” We’ve touched on it in two previous shows, but this is something that kids need repeated practice with, so we spend some time looking at that multiplying up strategy for division in this show.
We present the problem of 52 ÷ 4. It’s great to start by building the total of 52 with place value discs or base-10 blocks so you can model pulling out 40 or 4 groups of 10, showing that there are only 12 left, then seeing that 4 x 3 is 12. We really model the idea of seeing that focus number using the multiplying up strategy to help us, but also showing the repeated subtraction that’s happening when students are going through this process.
They are given four problems that are a little bit higher. We have 56 ÷ 14, can we use the multiplying up strategy? Well, maybe kids only know what 2 x 14 is, because they can do their doubles. The idea is to let them multiply up with the friendly numbers that make the most sense to that student.
As we move into show 306, students are again using Professor Barble with a multiplication problem so students can understand how to look at a visual model and create it. In 305, we learned how to do it, in 306, they’ll do it a bit more independently.
 The I Can statement is: I can divide within 100, where the quotient or the divisor is more than 20. We’re working with higher numbers here! We want kids to see that they have a better, hopefully more solid, understanding for division. So if I looked at something like 84 ÷ 4, could I do an estimate to see what would be too low of an answer, about right, or too high? Instead of rushing into a procedure, we want kids to actually think: What if I had 84 of something? What would be the reasoning? Why might something look that way?
The I Can statement is: I can divide within 100, where the quotient or the divisor is more than 20. We’re working with higher numbers here! We want kids to see that they have a better, hopefully more solid, understanding for division. So if I looked at something like 84 ÷ 4, could I do an estimate to see what would be too low of an answer, about right, or too high? Instead of rushing into a procedure, we want kids to actually think: What if I had 84 of something? What would be the reasoning? Why might something look that way?
We do another example problem of 78 ÷ 3 to show the concept of division with fair shares, but also how to do it with multiplying up. We practice with larger numbers like 96 ÷ 4. And we ask students which way they like to solve division problems: Do they like using the base-10 blocks? Or do they like using the idea of multiplying up?
 Students do an activity that involves understanding division to estimate and compare quotients. If kids are really just guessing or don’t have an understanding for what division is, this is where you’re really going to see that they have a lack of understanding because it’s going to be hard for them to estimate if they don’t know what it looks like.
Students do an activity that involves understanding division to estimate and compare quotients. If kids are really just guessing or don’t have an understanding for what division is, this is where you’re really going to see that they have a lack of understanding because it’s going to be hard for them to estimate if they don’t know what it looks like.
Membership Bonus!
If you’re an M³: Molding Math Mindset member, remember that you can download these presentations! How great would it be to have visual models all mapped our, ready to show in your virtual or face-to-face classroom? Maybe you show the actual show, or maybe you just want to download the PowerPoint and alter the numbers in the problems to fit what you’re doing – either way, they’re all yours to file and use!
(valid M³ Membership login required)



