Comparison bars are taught as early as first grade. They are actually the reason why the T-charts we talked about in an earlier post in this series can really confuse kids when they are problem solving.
 Sometimes, when we say “how many more does someone have?” kids identify the word more, but don’t realize that they’re comparing that amount to another amount to figure out the answer. Developmentally, the reason we start teaching this kind of problem solving in 1st grade is to help kids to understand the language in math. Problems that use comparison bars can involve lots of steps and can contain wording that is somewhat confusing, but in the end, the best thing about comparison bars is that they reall do help students to understand!
Sometimes, when we say “how many more does someone have?” kids identify the word more, but don’t realize that they’re comparing that amount to another amount to figure out the answer. Developmentally, the reason we start teaching this kind of problem solving in 1st grade is to help kids to understand the language in math. Problems that use comparison bars can involve lots of steps and can contain wording that is somewhat confusing, but in the end, the best thing about comparison bars is that they reall do help students to understand!
Often, we have two or three people involved in comparison bar problems. The change in the model drawing from part/whole problems is instead of using one bar, we will be using two bars for comparison. Comparison bars can also link themselves to algebra. Even as early as first and second grade, some of the problems could be related to algebraic equations. We’ll show a few examples of how this would work as we go through today’s post.
When we are drawing comparison bars, students will always start with the sentence stem that will answer the question asked in the problem. Every person in the problem gets their own bar, and students will label the who and what in the problem. And then it’s really important that kids draw a starting line once they have labelled their who and their what. We want the students to draw a line (as you’ll see in the sample drawings) because kids sometimes have a hard time lining up one bar to the other. When they have the starting line, they have a reference point so they can accurately line up the bars. Graph paper can help as well because kids can see the units and it’s a bit more organized, especially if kids are having a difficult time spatially on their paper.
When you start comparison bars with students, make sure you are using a manipulative that will help children understand the parts you are comparing. I love using Cuisenaire rods for this! There are lots of different kinds of Cuisenaire rods out there, but I particularly like the ones that interlock and have both a proportional side and a non-proportional side. (For more on proportional vs non-proportional, check our first post in this series!) We’d start off using the proportional side of these Cuisenaire rods, and the move into using the non-proportional size as appropriate.
Let’s tackle a problem:
Johnny went trick-or-treating and has five pieces of candy. His brother, Joey, has four more pieces of candy than Johnny. How many pieces do they have all together?
We can use Cuisenaire rods to help us develop that problem:

You can see that we’re using the yellow Cuisenaire rod for this problem, and if you look closely, you can see the individual hash marks that make this a proportional manipulative. When the students make Joey’s candy, they know he had the same amount as Johnny, so they’ll use the same yellow bar, but they know he had four more, so I used my purple colored Cuisenaire rods showing four additional individual units.
This is a great model for kids to see how to build comparison bars with real objects. I wouldn’t even really worry about kids getting the answer as much as them knowing what the question is asking. As we’ve talked about before, model drawings are more of a comprehension strategy for problem solving, so building these models simply by hearing or by reading stories in 1st and 2nd grade is excellent!
This kind of problem grows with students as they get older. Sometimes the problem will give you a total amount, and sometimes it won’t but it wants you to figure out the total. The part where this problem could change or be differentiated is that we could use higher numbers/amounts as the students get older. Maybe Johnny has 115 pieces of candy now, but Joey has 24 more. This calls for a non-proportional representation, so I can flip my Cuisenaire rods over (or use a different bar) so there aren’t lines delineating the units, but the drawing itself will look very similar to the first example. The smooth side indicates that the bar is representing a larger amount.

As the students progress, you want them to be able to use the Cusineaire rods in the Math Salad Bar, if they’re needed. After that, they can just do their drawings to help them solve their different problems.
Here’s another problem:
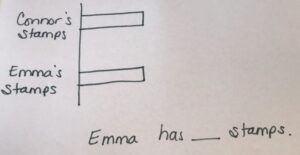
Connor and Emma were looking at their stamp collections. Together, they have 11 stamps. Emma has three more stamps than Connor. How many stamps does Emma have?
Before I even put any information from the problem into the model drawing, I first make sentence forms. “Emma has ___ stamps” and you can see I le
ft a spot for Connor’s stamps and Emma’s stamps in this picture.
I start with the two equal bars and then continue reading the problem and add in the information I find: 11 total stamps and Emma has 3 more. In order to find out what those two equal bars equal, I have to subtract the 3 from the 11 so that Connor and Emma have the same amount. I could say that X + (X + 3) = 11 or 2X + 3 = 11.
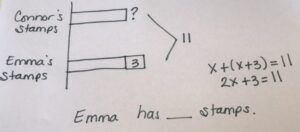
When I was a child doing algebra, my teacher told me if you add on the left side of the equation, you have to do the same on the right side. When I asked why, they never gave me an answer. They said it was to balance the equation, but it never made sense. It wasn’t until I started doin
g additive and comparison problems that it all made sense. The X is that bar that I drew originally that represents how many Connor and Emma had individually. In this problem, we have to take the 3 away from the 11, leaving us with 8. Then we could figure out that each of the two equal units actually equals 4. Then, to find out how many stamps Emma had, we have to take the 4 and add it to the 3 to find out that she had 7. This is actually a three step problem.
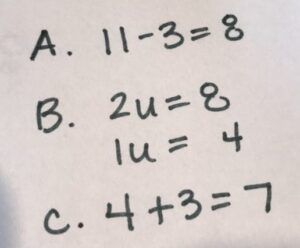
Another time you hear about using comparison bars is when you’re talking about people’s ages or miles driven.
Let’s look at a problem which involves people’s ages and is a 3-part comparison problem:
Harper is 8 years older than Cameron, and 2 years younger than Brady. If the total of their ages is 63 years, how old is Brady?
We’ll set up the model drawing to model exactly what the problem is asking. We’ll start by putting our sentence form, then the who and the what, and three equal bars to start with.
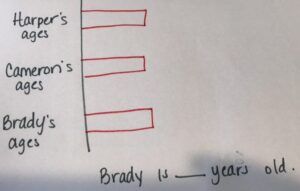
In order to start the problem, we put in equal bars for all three people involved to help us make more sense of it. This says that Harper is 8 years older than Cameron, so I’m going to add an 8 by Harper to show that she’s 8 years older than Cameron. Harper is 2 years younger than Brady, so I need to make Brady also have the 8, but he’ll have an additional 2.
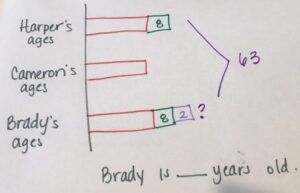
As we start to solve this, we see it’s actually a very lofty four-step problem! But when looking at it visually, it really makes sense.
We know the total of their ages is 63, we have to subtract 8 years for Harper because we know that she was 8 years older. And in fact, Brady is 10 years older than Cameron, so we subtract that 10 too. If we take 63 minus 18, we get 45. We figure out that the 3 units equal 45 together, so one unit equals 15. Last, we have to figure out what the question mark is, so we take 15 plus 10 and come up with 25 for Brady’s age.
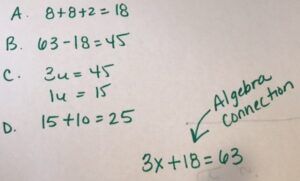
You can also see the algebraic equation for this problem = 3X + 18 = 63
Again, you subtract the 18 so you can get amount for the three equal bars.
Comparison bars, although they start off at a very young age back when we were talking about our pieces of candy with Johnny and Joey, can ramp up quite high for kids and involve lots of different operations. Usually, when children read this kind of problem, they go into a state of panic and don’t know where to start. Through the use of model drawings, bar models or tape diagrams kids can visually understand what the problem is asking and they can apply their number sense to what they’re doing.
All of our model drawing resources are excellent, but a specifically great resource that we recommend spending some significant time with is the model drawing books. Take time to teach kids how to do construct model drawings in a gradual progression, from the Cuisenaire rods to using lower numbers, and then using higher numbers.
Featured Products





I was just in a 2nd grade classroom and they were working on comparison bars. The kids were struggling because the numbers they were working with were so high. They were at a disadvantage because they didn’t have the foundation of model drawings from 1st grade. The teacher used a problem with something about someone having 26 ribbons and someone else having 14 less and how many did they have all together.
 When problems from the Model Drawing books are really complicated, it is ok to go down by lowering the numbers/amounts. We ended up bringing in Cuisenaire rods with this particular guided math group, and I had them bring the numbers down low so someone had 6 ribbons and someone else had 4 less. This way, the problem was more approachable so the kids felt like they could actually solve it. Once kids have an understanding of part/whole problems, this next layer is developmentally really great! This is taught as early as 1st grade all the way up.
When problems from the Model Drawing books are really complicated, it is ok to go down by lowering the numbers/amounts. We ended up bringing in Cuisenaire rods with this particular guided math group, and I had them bring the numbers down low so someone had 6 ribbons and someone else had 4 less. This way, the problem was more approachable so the kids felt like they could actually solve it. Once kids have an understanding of part/whole problems, this next layer is developmentally really great! This is taught as early as 1st grade all the way up.
A great resource for comparison problems is Thinking Blocks (click the Writing/Problem Solving tab). Whether you’re on Thinking Blocks Jr. or the Addition/Subtraction Thinking Blocks app, or the Thinking Blocks.com, click on Comparison Bars. Select the number of people you want in your problem (2 or 3), and solve!
Remember, you want to go slow to go fast. Kids will find problem solving much easier when they have a visual representation of what they’re being asked!

Make sure you join us next week for Multiplicative Comparison problems! Although that sounds really intimidating, if you understand how to do part/whole problems and comparison problems, these will be a breeze!






















