Multiplicative is a really hard word to say! It sounds super fancy and impressive, but in reality, if you understand how to do additive comparison problems, multiplicative problems are a snap!
 Using Manipulatives
Using Manipulatives
The biggest thing when learning to do multiplicative comparison problems, just as we talked about with learning additive comparison problems, is using manipulatives so kids can have a conceptual understanding of how the problems are drawn out. We want kids to understand what it means when the problem says something like “Joe collected three times as many rocks as Frank. All together, they collected 60 rocks.” Kids need help trying to understand what it means when someone has “three times” the amount, or “three more groups of” something than the other person. One of our favorite manipulatives to use with multiplicative problems are the 1” square tiles. These are available on our website, and they are made of foam, so they’re nice and quiet! They also come in a plastic version as well, if you choose.
We might not even actually use words as students start to practice with the tiles, instead, we could use A, B, and C. They might use the 1” square tiles. Until now, we’ve used a bar model, or a non-proportional unit bar, but in this case, we’re actually going to use squares and assign them a value of 1 unit each. In the first examples, we’ll make the unit squares worth 1, but later, the unit squares could be worth 15 or 45 or whatever the problem calls for.
The more practice you can give students with the 1” square tiles, the better. Allow the students who are more at risk and need a more conceptual look to go to the Math Salad Bar in the classroom to get the tiles if they’re needed to help them with the drawings. As the kids get better at these, they’ll start to be able to do more complex problems. Of course, the computation will get more complex because they’re doing division, so students can use a lot of different strategies that they might use in number talks, like multiplying up, partial quotients, decomposing using number bonds to divide and help them figure out where they’re going.
When using the 1” square tiles, a good rule of thumb is that less is more. We want students to use the least amount of tiles possible to show the model for the problem. The problem is not incorrect if students use more tiles, but it does make for more computation for the student to have to do.
If A were 6, B is ½ of A.
To build this problem, we want to start with A being worth 6. Then we can think about what the words are saying when it says B is ½ of A. Once we’re seeing kids playing with this concept, we can use lots of different things. You can start by putting in a variable, like we did in this problem, where students have to do ½ of that amount. You might say something like B is 2, A is 2 times B. Kids have to understand here is that we’re actually showing two groups. For B, I have 2, and I want A to show two groups, or two times, that amount.

Algebra Connection
In order to contribute to the understanding of X, you could choose not give a variable. For example, if I said A is 3 times B. I didn’t give the child a value to tell me what B is, so they have to put something in. You could put the value in as 1, which could make B = 1 and A =3. I could also make B = 2, which would make A = 6. Just remember that less is more! So if I were to say show me with A = 3 times B. You want the model to look like this:  Giving students lot of practice with the manipulatives instead of “real world” problems early on ( just staying with A and B, or even bringing in a variable of C) helps them build a foundation of understanding before they move on to more complex problems.
Giving students lot of practice with the manipulatives instead of “real world” problems early on ( just staying with A and B, or even bringing in a variable of C) helps them build a foundation of understanding before they move on to more complex problems.
Sometimes, when kids are faced with a problem like A = 3B, they will make B=1, but they’ll actually come up with A = 4 because they’re thinking of “four more” instead of “four times.” Students need to understand that “times” means “groups of.” If they know that, they know that if B is one group, then A is going to be three groups of what B is.
Depth of Understanding
Once kids get the hang of this the algebra connection, we can move them into understanding problems.
Sample Problem: Emma has 3 times as many crayons as Connor. If they had 60 crayons all together, how many crayons did Emma have?
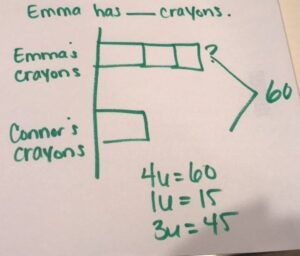
As we did last week, we’re going to follow our step-by-step for model drawing (as seen on the classroom posters), beginning with reading the entire problem. Have students read the individual sentences of the problem, while repeating key information back to you, and putting a slash in between each new piece of information. Step 2 is always going to be to create a sentence form to let us know what the problem is really asking us. Then, we label the “who” and the “what” in our drawing. Just like in additive comparison problems, multiplicative comparison problems will be represented on two to four bars.
Multiplicative comparison problems, because they’re much more complex), usually start to be taught more heavily in the 4th and 5th grades because they’re much more complex. A lot of times, they will involve two or more steps.
Let’s revisit Connor and Emma and their crayons. We can label the problem, show the parts that are there, and then actually use division to show how many equal groups of units we have. In this drawing, we have 4 equal units equaling 60. How much does one unit equal? 15. If we wanted to figure out how much Emma had, which is 3 times the amount, which would give her 45.
You can always make problems a little bit more complex and a little bit more difficult. They might not be asking how much each unit is, but instead they might ask how many more does someone have than someone else. So, on top of being about to figure out the division, they sometimes might be looking to see how many more. So, we could change the problem to ask “How many more crayons does Emma have than Connor?” In this case, Emma has 45 and Connor has 15, so Emma has 30 more crayons.
Decoding Complex Problems
 Let’s look at another scenario where we have boys and girls going on a field trip. There are 5 times as many boys as girls. If 120 kids are going, how more boys are going than girls?
Let’s look at another scenario where we have boys and girls going on a field trip. There are 5 times as many boys as girls. If 120 kids are going, how more boys are going than girls?
The language of this problem can sound very confusing to kids, and they wonder How am I going to find out how many boys are going? And how am I going to look at that in individual units?
In this case, we’re going to make one unit for the girls and for the boys, we’re going to show that there are 5 times that amount. We can use the 1” square tiles or draw a picture so the students can see that there are 5 boxes for the boys and 1 box for the girls. The total is 120, but it wants to know the difference, meaning how many more boys are there than girls going on the field trip. The question mark shows that we are looking for that difference.
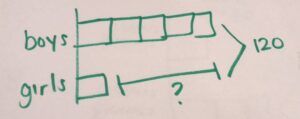
Multiplicative comparison model drawing really helps kids break down much harder problems that they might not have been able to attack otherwise. Drawing out the problem helps kids look at the idea of “times of” or “repeating a group of.”
Additional Resources
![]()
Thinking Blocks is a great resource for multiplicative comparison problems as well. They have a multiplication/division app that matches comparison bars for multiplication and division problems. They have some with two parts, some with three parts, some that involve more operations. Giving kids consistent, targeted practice within each of the types of problems that fall under the multiplicative comparison umbrella will help kids become more proficient instead of just exposing them to a cross section of all the different types of story problems and hoping that they’ll just guess/check or figure out some strategy. You really want to spend several weeks, or even months in the 4th/5th grade classrooms, doing multiplicative comparison problems, breaking them down into achievable steps and gradually building to become more complex.
In these 4th and 5th grade especially, kids need to be problem solving every day. If you’re doing a Math with Writing station, make sure kids have a journal template (here is ours you can use for free!) and insert your own problem from your book or wherever you got it. Get kids comfortable with the fancy words “multiplicative comparison” and help them understand that they’re showing a certain number of “times” the amount, or showing “groups of” and then repeating it. They have a better understanding of how the more complex problems can be written.
We still have a sale still going on for all of our model drawing products: 10% off of the items that support model drawing with the code: SISMODEL We have a book of word problems written for additional practice for every grade. We also carry a book of More Challenging Word Problems that is most appropriate for grades 6-9 so you have access to higher level story problems for when the kids are ready. Each of the books in the upper grades will spend a little bit of time on multiplicative comparison problems. Remember to bring the numbers down to be more compatible or numbers that are a little bit easier to divide and multiply until they get the hang of what they’re doing with it.
Featured Products





Next week: The grand finale: Fraction Problems for Model Drawing. This is the last one in our Problem Solving Series, so don’t miss it!






















