In this post, we move from just talking about math problems like we were doing in Kindergarten, into the 1st grade classroom where kids are able to answer a variety of part/whole problems.

As we’ve talked about in the previous two posts in this series (Intro to Model Drawings and The Early Years), model drawings have different names: bar models, tape diagrams and model drawings. These are great comprehension strategies to help students learn to decode what questions are asking.
Part/whole problems comprise one fifth of the type of problems students will encounter in elementary school. These problems often will use all operations (addition, subtraction, multiplication, division) and will even extend to missing addends, 3-part part/whole problems and multi-step part/whole problems. A child in 1st grade will learn part/whole problems with addition, subtraction, and missing addends, as well as 2-part part/whole problems and the addition of a third character into the story problem.
Let’s start with a typical problem:
If Shannon has 8 pieces of an orange, and Suzy has 5 pieces of oranges, how many do they have altogether?
Teachers often want to use individual unifix cubes to represent the problem. With this level of a problem, individual cubes are fine, but after a while, the quantities in problems will continue to get larger. Maybe instead of 5, Suzy might have 26 pieces of something and her friend might have 42. These numbers become much more challenging to represent individually.
 In our first grade model drawing book (Word Problems for Model Drawing: Level 1), we follow a very developmentally appropriate method to scaffold our students away from the need to individually represent objects in a problem. In the book, you’ll see that students do start off with actual drawings of the objects. So, if the people in the problem have flowers, the student will actually see flowers drawn. As you go through the book, the flowers will eventually be put into square units, so they will draw a square unit around the flower to represent the value of how many flowers there are. After a while, the picture of the flower goes away and students are left with an empty individual unit to represent the value. After they start to understand that concept, the book transitions away from proportional units altogether into a non-proportional bar. The bar can represent any number. Typically a bar that is shorter will represent a smaller value, and a longer bar will represent something with a higher value.
In our first grade model drawing book (Word Problems for Model Drawing: Level 1), we follow a very developmentally appropriate method to scaffold our students away from the need to individually represent objects in a problem. In the book, you’ll see that students do start off with actual drawings of the objects. So, if the people in the problem have flowers, the student will actually see flowers drawn. As you go through the book, the flowers will eventually be put into square units, so they will draw a square unit around the flower to represent the value of how many flowers there are. After a while, the picture of the flower goes away and students are left with an empty individual unit to represent the value. After they start to understand that concept, the book transitions away from proportional units altogether into a non-proportional bar. The bar can represent any number. Typically a bar that is shorter will represent a smaller value, and a longer bar will represent something with a higher value.
In a typical 1st grade classroom, we like to scaffold as much as possible so students start to understand that, not only do numbers and words have a connection to the real world, but there are words that ask them to do specific operations. In the first blog, we talked about how , sometimes we see T-charts with plus/minus, multiply/divide on the wall, and we train kids to watch out for certain language in a story problem that will trigger an action. These are ok for part/whole problems because those are typically what is being asked. But as soon as you get asked more than one step, “altogether” might not mean that you just add the two numbers.
 We really want to make sure we take the time to go through the step-by-step model drawing process, just like we have on our model drawing poster and as we have on the student checklist. Kids first read the entire problem, then go through and put slashes in when new pieces of information are given, write a sentence form to tell what is actually being asked, identify the who or the what is in the system, make their bar unit, and wait to do their computation until step six. Younger learners want to get right to answer, but it’s really important to adhere to the process and “go slow to go fast.” Kids have to understand what the problem is asking so that when problems become more complex, they have a consistent system in place to help them attack them with confidence.
We really want to make sure we take the time to go through the step-by-step model drawing process, just like we have on our model drawing poster and as we have on the student checklist. Kids first read the entire problem, then go through and put slashes in when new pieces of information are given, write a sentence form to tell what is actually being asked, identify the who or the what is in the system, make their bar unit, and wait to do their computation until step six. Younger learners want to get right to answer, but it’s really important to adhere to the process and “go slow to go fast.” Kids have to understand what the problem is asking so that when problems become more complex, they have a consistent system in place to help them attack them with confidence.
Types of Part/Whole Problems
Part/Whole Addition. Start by labelling the who or the what. Then have the kids use a starting line to actually build their bar for their bar drawing. You technically don’t have to do the drawing until you get to comparison bars, but it’s nice to have in a scenario like this:
Shannon has 5 pieces of candy, and Sarah has 9 pieces of candy. How many pieces of candy do they have all together?
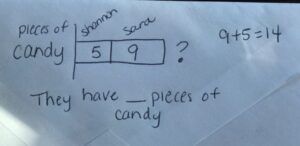
We start by labelling the candy (the what), then draw the bar model to represent how many Shannon has and how many Sarah has. We can actually chunk the bar, so if Shannon only had five, we can put the line a little bit to the left to make the bar larger for Sarah, who has nine. At the top, we would label who has 5 and who has 9 pieces of candy. And our question mark would be at the end.
For this type of problem, the quantities can get up quite a bit higher, but the bar graph is non-proportional so will work regardless of the number quantity. For example, Shannon might have 52 pieces of candy after Halloween, but Sarah has 92. How many altogether? The model drawing will look similar, but it will simply contain higher numbers.
Part/Whole Subtraction. When we do a part/whole subtraction problem, we typically use a diagonal slash to say that something was taken away in the problem. Let’s look at a scenario:
Shannon has 14 pieces of candy and her brother Patrick ate 3 pieces. How many pieces of candy does Shannon have left?

This is similar to part/whole addition in that we still identify the who (Shannon) and the what (Shannon’s candy). At the end of the individual bar, we would put the total, since we know it equals 14. Since her brother ate some, we’re going to proportion the bar, put a diagonal slash through it to say that he actually ate three pieces. At the top, we’re going to label that part “eaten,” and put a question mark for how many are left.
This can also definitely ramp up much higher. For example, after Halloween, Shannon had 126 pieces of candy, and she at 42 of the pieces. How many are left? When we get to more complex problems, there will also be some problems with missing addends. The thing to remember is that we only represent in the model drawing the things that the problem is actually saying. Even if they want to write the answer in the box, the idea is that the model drawing is a drawing of just what the words are asking in order to help kids decode them.
Kids in upper grades can also do lots of part/whole problems with addition and subtraction, but they’ll use higher numbers and might also include more steps.
The best app to use for part/whole addition and subtraction is ThinkingBlocks.com via the Math Playground. This site has many videos showing part/whole addition and subtraction, as well as missing addends. Check out our resource page for the link and for all more model drawing resources.
Part/Whole Multiplication.
Here’s a sample problem:
1 spider has 8 legs. How many legs do 5 spiders have?
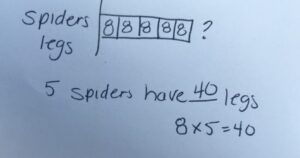 In this particular model drawing, we create individual unit bars when we’re talking about multiplication. We’ll have a bar written where we’re talking about spiders’ legs and we’ll go ahead and make the unit bar and we’ll talk about how many units we have. We have five spiders, so we’re going to make five squares. We know that one square equals eight. The question mark goes at the end of the model drawing because we want to know how many legs five spiders have.
In this particular model drawing, we create individual unit bars when we’re talking about multiplication. We’ll have a bar written where we’re talking about spiders’ legs and we’ll go ahead and make the unit bar and we’ll talk about how many units we have. We have five spiders, so we’re going to make five squares. We know that one square equals eight. The question mark goes at the end of the model drawing because we want to know how many legs five spiders have.
Multiplication can get more complex very easily, using bigger numbers or having kids divide. Remember, during the computation phase, kids will have different ways to figure out 5 groups of 8 and they can do all kinds of things, but ultimately we want the model drawings to look a certain way so they start to understand what a part/whole multiplication problem looks like.
Part/Whole Division Problems.
This type of problems have their own unique appearance.
I looked out and saw 40 spider legs. One spider has 8 legs, so how many spiders do I see in all?
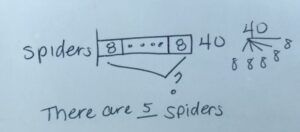 In this case, put your starting line, and draw the bar. At the end, you’ll write 40, since that’s the total and how much you have. We essential want to know how many groups of 8 are in that bar of 40. A model drawing for division takes the unit, puts that number first, and then puts a “dot dot dot” meaning “how many of these groups of 8 are in there”? We like to put the 8 at the end of the bar unit so that students know that there might be a remainder. We’re looking to find out how many equal groups of 8 could fit into that number. In this case, you want the question mark to go over all of those bars because we need to figure out how many total spiders there will be if there were 40 legs.
In this case, put your starting line, and draw the bar. At the end, you’ll write 40, since that’s the total and how much you have. We essential want to know how many groups of 8 are in that bar of 40. A model drawing for division takes the unit, puts that number first, and then puts a “dot dot dot” meaning “how many of these groups of 8 are in there”? We like to put the 8 at the end of the bar unit so that students know that there might be a remainder. We’re looking to find out how many equal groups of 8 could fit into that number. In this case, you want the question mark to go over all of those bars because we need to figure out how many total spiders there will be if there were 40 legs.
The Bottom Line
In essence, when we look at part/whole problems, although they look very simplistic, they’re the foundation of what students need to understand to continue. Many of our part/whole problems can become very complex by using larger numbers, requiring kids to divide by larger groups, add or subtract and become three-part problems.
![]()
You can find a range of problems on Thinkingblocks.com. If you want to do multiplication and division, click on the multiplication/division section. You’re looking at part/whole problems or you can select two-part problems to make things more complex. The idea is when problems become harder, you want all of these to be on one model drawing for a child to figure out how to go about solving these problems.
The most important thing to remember is to be using our journal templates (PreK/K and Simple) as well as our Step-by-Step Model Drawing poster. For continued resources to help you with model drawing, we highly recommend our Step-by-Step Model Drawing book, as well as our 1st-6th grade series of model drawing books. These give you really great problems, as well as an answer key. So if you’re new to model drawings, you’ll want to be able to use these as a support to help you.
Eventually, as you become better at finding part/whole problems, you’ll be able to enter this process into any math series or any story problem that you’re using. Remember that these problems can become much more complex, so it’s much better for students (even older students!) go down to easier problems, and then help them work their way up.
Check out our problem solving kits here. You’ll notice that we always provide a teacher with the model drawing book for the grade below to help them scaffold for students that are learning.
I can’t tell you how powerful this problem solving process is for schools that in our Math Initiative project. Many of our schools start learning problem solving through model drawing in 1st grade and can go all the way up through 8th grade. There are students taking our state test that were actually using the model drawing process because the poster was up in the classroom, they were consistently provided with instruction in using the process with all different types of problems, and they were also given the student step-by-step checklist. Consistency is the key. When students are working on problems five days a week (in grades 2-5), and students start to understand the early development of model drawing. Even in the second semester of the 1st grade year, it really helps students as problems become more complex and math continues.
Join us next week for a look at comparison bars!
Comment on our blog if you’ve been using model drawings! We want to hear what they’ve done for you as an adult learner, as well as for your students!
Featured Products



























