Fractions, as we know, is a very hard area for students to acquire conceptual understanding. When reading a word problem involving fractions, most kids panic because they don’t know where to start.
 Thoughts like “we should skip count and find a common denominator” or “is the problem asking how many we should do all together?” run through their heads. The hardest part about fraction word problems is that they are usually multi-step and sometimes the words used are scarier than what the problem is actually saying.
Thoughts like “we should skip count and find a common denominator” or “is the problem asking how many we should do all together?” run through their heads. The hardest part about fraction word problems is that they are usually multi-step and sometimes the words used are scarier than what the problem is actually saying.
So, when it comes to these kinds of problems, we want to help kids break down the problem. We can help them go through the process of reading the whole problem and putting lines in the problem when they get new pieces of information and then we can help them be able to build the problem within their model drawing.
Manipulatives for Fraction Model Drawing
 I like using Cuisenaire rods (like we did with additive comparison problems) and 1” square tiles (like we did with multiplicative comparison problems). In most model drawings that we’ve done, like in the multiplicative problems, we use individual square units, That’s usually what we see with fractions too because the students will be using the bar as a whole and dividing the bar into the amount of equal pieces in the fractional part. For example, if the problem was saying ⅖ of something, the student would draw in a bar and turn it into five equal units by drawing four lines, and then shading in two of them.
I like using Cuisenaire rods (like we did with additive comparison problems) and 1” square tiles (like we did with multiplicative comparison problems). In most model drawings that we’ve done, like in the multiplicative problems, we use individual square units, That’s usually what we see with fractions too because the students will be using the bar as a whole and dividing the bar into the amount of equal pieces in the fractional part. For example, if the problem was saying ⅖ of something, the student would draw in a bar and turn it into five equal units by drawing four lines, and then shading in two of them.
Introducing Fraction Model Drawing
It’s always a good idea to get kids to play and explore the idea o
f what they’re going to do before you actually put words into it. A good way to do this is with mystery numbers, where students have to see if they can guess what the mystery number is going to be by giving them clues about the number and its fractional parts.
The first problem we’ll look at is called “Guess My Number.”
If I say that ⅗ of my number equals 24, what is my actual number?
When most kids look at a problem like that, it’s hard for them to fathom what that actually would mean or what the units would even be. As with all of our word problems, we want to start with our who and our what. The who is the mystery number itself, so we draw a bar showing the whole unit. If we wanted to show that ⅗ of the number is 24, we would break the bar into five equal units by drawing four lines, and shading in three of the units to represent ⅗ of the number. Above it, we’ll put a bracket and the number 24 to show that those three equal units are a total of 24 out of the five units.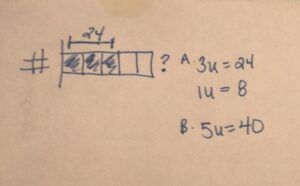
From there, this is similar to the multiplicative comparison problems because students have to figure out how much each unit is worth within the whole number. In this case, if we had three units equalling 24, we could divide by three and see that one unit is equal to 8. Kids can easily figure out that, if each unit is worth 8 and there are 5 total units, and the whole number in the problem was 40.
When I look at a drawing of this problem, it makes something that seems like it was very intimidating seem pretty simple. You can see in the drawing above how we solve that problem to quickly understand what the mystery number is.
Fraction Model Drawings with Two Question Marks
We could make these problems a little bit more complicated by changing the words, especially if we’re teaching in upper elementary.
⅖ of the number is 32. If that is the case, what is ¾ of the number?
In this case, they’re asking the kids to solve this problem that has two questions marks. Students will need to figure out how to solve for the 5ths, then actually figure out what the mystery number is before they can divide it into the fractional units (4ths) that the problem is asking.
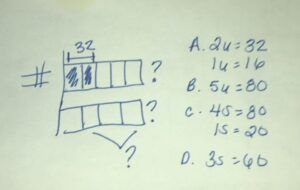
So, so solve this problem, we start by drawing a unit bar and dividing the unit bar into equal pieces based on the fractional amount. To show ⅖, will make five units, shading in two of the fifths to demonstrate that those two units represent 32. A question mark needs to go at the end of this bar because we do need to figure out the mystery number first based on the information we have before we can start worrying about dividing it into fourths. Then, after we figure out what the mystery number is, we can draw a second bar, making it the same length as the bar above it. But this time we can divide into four equal units because the question wants to know what ¾ of the number would be. We already know, once we figure out the mystery number, how much that unit bar is going to equal, so we can put in that value and then solve for the ¾ of the unit.
Doing the math: If we have ⅖ and the number is 32, that makes each individual unit worth 16. If I were to do 16 x 5, all five of the boxes totals 80. Dividing a new bar of equal length into 4 equal units will tell us that each equal unit is worth 20. The problem is asking for ¾ of the mystery number, and 3 units worth 20 each equals 60. In our example, the math steps are labelled A, B, C, D. It’s important for students to label the steps that they’re doing in problem solving to go slow with each of the steps to make sure they’re including everything the problem is asking. In fractions, and when we were doing multiplicative comparison problems, I can use the letter u to represent a unit. You could also use an x if you wanted to bring in the algebraic part to this.
Fraction Model Drawing Story Problems
Once kids have had a lot of experience doing model drawings with fraction problems without words, it’s time to move into story problems that have would actually have words or scenarios that would go along with the problem. When you’re doing different kinds of fractional problems, it can be fun to create stories that go along with the kids’ understanding of the parts of fractions.
Don’t skip straight to this part or rush through it! If you skip the part where kids are guessing the number, or you don’t help kids to understand what fraction word problems really are, it usually will result in students feeling really overwhelmed and wanting to give up. Taking time to slow this process down time will help students answer more challenging problems.
Ruth made 3 dozen candies. ⅓ of them were red, ¾ of the remainder were yellow, and the rest were blue. How many blue candies did Ruth make?
In this problem, we’re going to have one unit bar with three individual units, and label the first unit with an R. ⅔ of the candies remain, but the problem said that ¾ of them were yellow. We need to take those last two boxes and redraw them into four individual boxes to show the 4ths. We can go ahead and put a Y inside three of those four subunits because it’s showing that those are yellow. The last box will get an B because those are blue. The question is how many are blue?
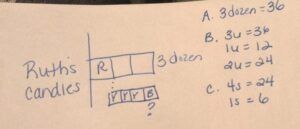
First of all, we have to recognize how many three dozen is (36). The three units equal 36, so one unit would equal 12, which tells us that Ruth made 12 red candies. That first step is pretty simple because you can look at 3 equal dozen and know that there are three parts. The trickier part is finding ¾ of the remainder. We know that the remainder is the same as two units, which equals 24, and those four subunits will also equal 24. To figure out how many each of those subunits would be, we would take 24 and divide it by 4 to tell us that each of those units equal 6, so Ruth made 6 blue candies.
Resources for Fraction Model Drawings
![]() There are lots of different examples on ThinkingBlocks.com. You can click on fractions and see different types of problems that kids can use as models and see several videos. All of our model drawing materials are great resources to help teachers understand how to do fractions in a way that helps students actually get it. Check out the Word Problems for Model Drawing Books for Grade 3, Grade 4, Grade 5, and Grade 6. In addition, we have our Step-by-Step Model Drawing book and Model Drawing for Challenging Word Problems Book for grades 6-9.
There are lots of different examples on ThinkingBlocks.com. You can click on fractions and see different types of problems that kids can use as models and see several videos. All of our model drawing materials are great resources to help teachers understand how to do fractions in a way that helps students actually get it. Check out the Word Problems for Model Drawing Books for Grade 3, Grade 4, Grade 5, and Grade 6. In addition, we have our Step-by-Step Model Drawing book and Model Drawing for Challenging Word Problems Book for grades 6-9.
You made it! This is the 6th and final post in our in Problem Solving Series! We hope you’ve enjoyed these posts and that you’ll be able to use theme as resources for your classroom and district!
Missed previous posts?
Problem Solving Series: Introduction to Model Drawings
Problem Solving Series: The Early Years
Problem Solving Series: Part/Whole Problems for Model Drawings
Problem Solving Series: Comparison Model Drawings (Addition/Subtraction)
Problem Solving Series: Multiplicative Comparison Problems for Model Drawings
Featured Products



























