Meet our newest Math Might Friend – Professor Barble!
 Let’s face it – most teachers feel like we drag our students through problem solving. Maybe we’ve taught using some variation of the CUBES method, which has students circle the numbers, underline the important words and then decide what operation to to use. This works really well…IF it’s a simple addition or subtraction problem that actually has those clue words like “all together” that the kids are looking for.
Let’s face it – most teachers feel like we drag our students through problem solving. Maybe we’ve taught using some variation of the CUBES method, which has students circle the numbers, underline the important words and then decide what operation to to use. This works really well…IF it’s a simple addition or subtraction problem that actually has those clue words like “all together” that the kids are looking for.
But, when the problems get more complicated and you ask what operation we should use, kids often begin to engage in a “guess/check” game. “Add??” they’ll say, with a large influx in their voice, turning their answer into a question. They gauge the teacher’s reaction to see if they were right. If the teacher says, “Hmm…is that what you think we need to do?” students are quick to jump to the next guess. “No! I think we should…subtract??” and so on until an agreement has been reached. Or, students might take the operation of the week (multiplication for example), and automatically take the two numbers in the problem, multiply them, and offer their answer without reading the actual problem.
The bottom line is that kids don’t always feel confident when it comes to story problems. They rely on us as adults to help them through it, when sometimes we aren’t all that confident either.
 Enter: Professor Barble, the newest resident of Mathville! He is a little bit different than the other citizens of Mathville. Instead of solving algorithms, he faces real life situations that he has to solve, with the help of his Math Mights friends. Professor Barble loves to hike throughout the fields of Mathville, climb large mountains, and discover complicated problems in which he has to do a little bit of thinking to figure out what he is thinking about.
Enter: Professor Barble, the newest resident of Mathville! He is a little bit different than the other citizens of Mathville. Instead of solving algorithms, he faces real life situations that he has to solve, with the help of his Math Mights friends. Professor Barble loves to hike throughout the fields of Mathville, climb large mountains, and discover complicated problems in which he has to do a little bit of thinking to figure out what he is thinking about.
Over the years, he has really struggled with trying to do problem solving, because he is very quick to jump to thinking of adding or subtracting or multiplying or dividing when he encounters a problem. When he encounters word problems that are more complicated during his hikes, he struggles. In the past, he’s tried just looking at the numbers and circling important words. He’s tried “guess and check.” But he still struggled.
I think we can all relate to Professor Barble, but we can also see what he’s done to help himself become more wise as he approaches word problems. Check out the newest gadget that he’s added to his hat – a vertical pole that comes out of the top. As he comes to a problem, he stops, pushes his magical button, and this line comes out of his hat to help him to stop to think about what the problem is actually asking. It reminds him that, before he goes immediately to the computation, he needs to think of the step-by-step model drawing process that he would go through. He understands now that the computation piece really doesn’t come until step 6. Professor Barble wants kids to know that story problems are not designed to just guess and check and do a bunch of arithmetic, but to really apply comprehension strategies.
Reading Comprehension…in Math??
As we begin a series on model drawings that will feature Professor Barble, we want to emphasize that we can’t teach kids conditions in math. The CUBES method isn’t as effective as we once thought because, while it works for part-whole problems with words like all together and difference, those standard part-whole problems only make up about a fifth of the problems students are going to encounter in their education career. If you look at the 8 mathematical practices and the standards for 21st century learning, there are comparison problems, multi-step problems, and they just aren’t as simplistic as we would want. Therefore, we can’t teach students that you’re just going to circle the numbers and underline the words and you’ll get the answer, or that you can just guess which operation to use. It’s more than that.
Professor Barble wants to help us understand that reading comprehension is really the essential piece when it comes to problem solving. This is a very intentional strategy, and in my opinion, that is exactly what we need in our schools and classrooms when it comes to the comprehension aspect of math.
His name “Barble” comes from the idea of a unit bar, which is a very effective tool to use in solving word problems because it is non-proportional (not drawn to actual size). This unit bar model, model drawing, or tape diagram (whatever you call it, they all refer to the same concept!) can represent whatever you need it to! It is a universal strategy that can be used for anything from addition part-whole problems all the way up through ratios and proportions in middle school.
Coding Story Problems
The pictures that follow, featuring Professor Barble, are going to be part of a new digital download designed for students and teachers. They all show different kinds of problems within the context of the same numbers and story: Professor Barble and his students finding diamonds. Before they get into solving actual problems, these pictures will challenge students to create the story that goes along with the model drawing that is pictured.
Many teachers who attend our trainings do well with understanding model drawings, but then they go back to their Math Expressions or Go Math or Eureka Math and the problems aren’t coded. There are usually a few different problems and it’s overwhelming to the teacher and the students trying to figure out what types of problems they have.
In upcoming blogs, we’ll dive deeper into the coding system and how it really empowers teachers to feel like they can pick up any story problem and know how to do a bar model of it, instead of being tied by the sample problems we’ve done in the workshops.
Once the students understand, if they’re focusing on additive comparison Bar or focusing on a multiplicative comparison or part-whole subtraction, then you can do more of a mixed review where kids would understand the different types of problems.
Want to learn more? Join us for our Molding Math Mindsets Model Drawing Workshop (Grades 1-5) in Michigan – March 7, 2019! This additional session was added due to popular demand – sign up now so you don’t miss it!
In the Field with Professor Barble
Take a look at the picture below. Based on the model drawing, what would the story problem look like?

Professor Barble and his students were collecting diamonds. On Monday they collected 42. On Tuesday they collected 24. How many do they have all together?
We would label that as a PWA (part-whole addition problem). This is a part-part-total problem. Most people don’t label story problems, but because we’re so intensely working with schools, one of the things I’ve found is that if teachers know it’s in the part-whole family, they kind of know the type of problem that they would be setting up for that.

Professor Barble and his students collected 42 diamonds. They dropped 24. How many do they have left.
This one would be PWS (part-whole subtraction), and in this problem, something is being taken away, which is why we use a diagonal slash.

Professor Barble and his students had to collect 42 diamonds. So far, they have collected 24. How many do they have left to collect?
This is a PWMA (part-whole missing addend). The idea behind this is that the students can understand that the problem has a missing part. Someone might count up from 24 to 42 so it’s not necessarily the operation of subtraction because there’s nothing actually being taken away in the problem, even though you could use that operation to find the missing number. We don’t use a diagonal slash when we’re doing missing addends because even though it might appear that we do subtraction, some kids might count up and the words didn’t say that anything was taken away.
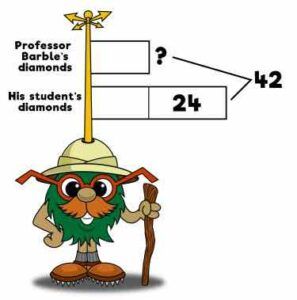
Professor Barble and his students collected 42 diamonds. His students collected 24 more than Professor Barble. How many diamonds did Professor Barble collect?
This is an AC (additive comparison), meaning we give each person an equal bar, and we add a bar to one or the other to show that someone has more or less than the same amount. This is an important skill for kids to learn because sometimes they learn to circles the numbers and underline the important words. However, if we were to circle these numbers and underline important words in this problem, it really wouldn’t help us solve this problem. It isn’t that the students just have 24 diamonds. You have to take the total number and subtract it, which is really algebraic. It could be written as 2x+24 =42. This really helps kids get set up for algebra at a young age with problems like this.
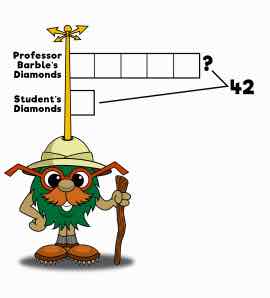
Professor Barble found five times as many diamonds as his students. If, all together, they found 42, how many did Professor Barble find?
The last type of problem is multiplicative comparison (MC), where someone has so many times the amount the other person has. Professor Barble’s bar has five squares and his students have one to illustrate this. In this problem, you could also use 1” square tiles to show this physically. Once students see all the squares together (six total), they can figure out that each square is worth seven.
A lot of times, when kids see the language of “something is five times as big as something” they really don’t understand what’s going on in the problem. But when you look at the picture, they can immediately say it makes so much more sense! That’s really the whole idea behind model drawings. It isn’t a math strategy necessarily, it’s a reading comprehension strategy to help you know how to do the computation strategy. Instead of being paralyzed with fear, we want to help teachers and students know that, when it says “so many times as big,” they can use that to identify that we’re going to be doing a multiplicative comparison problem.
Vertical Strategy for Problem Solving
Obviously this doesn’t cover every single type of word problem. There is still part-whole division, part-whole multiplication, part-whole multi-step, additive-multiplicative, fractions (although we do have a sample on the cover of Professor Barble’s publication), etc.
 Story problems inevitably send kids into sheer panic mode because they’re thinking, I have no idea how to solve this, I don’t know what to do, I don’t even know what the words are asking. But when we slow down and have Professor Barble hit his button, put up his sturdy bar, and rethink the problem out slowly before we’re worried about adding, subtracting, multiplying or dividing, it provides a much more efficient strategy.
Story problems inevitably send kids into sheer panic mode because they’re thinking, I have no idea how to solve this, I don’t know what to do, I don’t even know what the words are asking. But when we slow down and have Professor Barble hit his button, put up his sturdy bar, and rethink the problem out slowly before we’re worried about adding, subtracting, multiplying or dividing, it provides a much more efficient strategy.
We try to stress to students and teachers that this isn’t just work for the one grade level. Professor Barble’s strategy works consistently for first through eighth grade because kids in 6th, 7th, and 8th grade are still doing this, but with ratios and proportions. As is the goal with the rest of the Math Mights, Professor Barble continues to help create a common language in schools and it provides what I call a vertical strategy for schools that you can use across multiple grade levels. The step-by-step model drawing poster is really a pivotal piece to that strategy, because when a child walks into a classroom, they see something familiar and think, Hey, we had that poster! I remember Professor Barble! I remember stopping and thinking and what our journal template looks like!
The strategy also serves to increase student achievement scores in the area of problem solving, especially considering that our state tests are made up of 75% communicative reasoning, real life situations, and problem solving. It is a really great fit for 21st century schools to have this.
If you’re in Michigan, join us at our upcoming workshop to learn more! If you need customized training back in your own district, we’re starting to book for the 2019-2020 school year. We anticipate having a waiting list this year, so don’t get left out!




