The popular topic for PD sessions this spring? Fractions!
When we look at what kids have to know about fractions now, it’s very different from when you and I were growing up! We heard things like, “Don’t ask why, just invert and multiply,” and so we obediently multiplied without really understand the idea behind that concept.
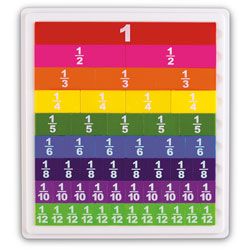In our 21st Century Math Initiative, we’ve been doing a lot of coaching in 4th and 5th grade classrooms helping implement 21st century standards and helping teachers understand conceptually what fractions actually mean, from the beginning stages of foundational understanding to looking at things like equivalent fractions, comparing fractions and addition, subtraction, multiplication, and division of fractions.
This video by Graham Fletcher from gfletchy.com, does a really good job of understanding the progression of fractions. We talk about “peeling back the layers” to diagnose various stages in a child’s development. When we look at kids in the area of number sense or numeracy, it feels like we’re able to peel back those layers and really target the steps in the development of this skill. But what do the layers look like for fractions? In this video, Fletcher breaks down a progression of what a first grader should know about fractions all the way up to what a fourth grader should know, with the majority of fraction instruction happening in third grade.
Another great resource for fractions when we’re thinking of our understanding of fractions is what kids need to know for the state test. When we look at the 8 Mathematical Practices and their application, a lot of tests today are not looking at whether the child can find the right answer. They’re asking questions like “Which picture shows 5 x ¾?” which really means “Which picture shows five groups of ¾?” Many times, students end up learning procedures for concepts they don’t really understand.
It’s really timely to look at the progression of fractions, and, as teachers, to take some time to understand what fractions are really about as we strive to help our students develop the same understanding.
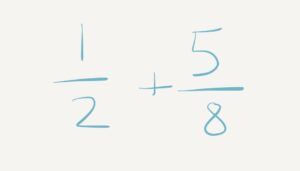
In many of our recent workshops, we take teachers on a journey of understanding the development of fractions. Even to do a number talk on fractions, teachers have to understand. Let’s say I did a number talk on fractions asking you to solve ½ + ⅝. Out of habit, we typically start applying a process we learned and start skip counting to find the common denominator, which would be eight. We do some multiplication to turn that half into a different fraction that we can then add together.. But in reality, we want to look at what fractions really look like, and actually have discussions about how we could solve the problem. There are lots of ways to solve ½ + ⅝!
One way might be to look at the ⅝ and anchor kids to understand what a half is. We help them learn about the fractions that are equivalent to ½, like 3/6 and 4/8 and 6/12. If you’re looking at ⅝, you can see that ⅝ is one more than 4/8, which is another name for one half, so you could decompose ⅝ into 4/8 and ⅛. You can then add the 4/8 to the other half to get your whole and you’re left with 1 ⅛. We can show this in number bonds by showing decomposing.
Some kids might also look at this in a linear method, or a number line. Students might have originally labelled their number line with labels like 0, ½, 1. We could decide to turn the hashes on the number line into 8s, so students can start by renaming that half-way point on the number line into 4/8. The rest of the points on their number line range between 0 and half (⅛, 2/8, ⅜), rename ½ to 4/8, and then continue renaming the rest of the hashes on the number line (⅝, 6/8, ⅞, 8/8) as redeeming one whole. Kids can use number lines as a strategy to help them add fractions with an uncommon denominator by hoping from the zero over to ½ (a.k.a. 4/8) and then add on their additional ⅝ to figure out how far over one they would be. A lot of kids have a hard time dealing with estimating to know Should that number line be from 0-1? 0-2? 0-1.5? In this case, we’re looking at ½ + ⅝, kids would hopefully estimate that their answers are going to be greater than one because they can look at ⅝ and see that it is larger than 4/8, which is equal to half, so I know ⅝ will be more than half.
Another way a student might be thinking about the problem is renaming the fraction to match the other fractions. So, if I had ½ + ⅝, I might decide to rename the ½ into 4/8, because then I could add 4/8 and 4/8 (which I pulled out of the original ⅝). This equals 8/8, which is one whole, and then we have ⅛ left over, so we get 1 ⅛.
The idea that we learned that the only way to do fractions was to skip count and find the answer is so outdated! There is so much more meat to the instruction in today’s world based on what kids have to understand about fractions. Sometimes, I’ll even give kids the answer to the fraction problem and have them prove it with a manipulative and show me how they know it’s correct. Lots of students have a hard time with this.
In this next blog series, we’re going to spend some time examining fractions and looking at what manipulatives might be used for certain situations and concepts in fractions, whether we’re looking at equivalent fractions or addition and subtraction of fractions and so on.
Resources
A really great resource is this book, Number Talks: Fractions, Percents, and Decimals by Sherry Parrish, which contains such great videos and contributes to such rich understanding (we blogged about it here!). There is also a companion you can download from the Math Solutions page using the number lines on Math Solutions.com
Listening to some of the reasoning and how kids understand benchmark fractions, and how they end up creating different ways to solve the problem and then communicate their reasoning is pretty profound.
Two other books:
- Beyond Pizzas and Pies: Ten Essential Skills to Help Teach Fractions (we blogged about it here!) – this is a great book with a lot of video examples that break everything down for you!
- Beyond Invert and Multiply – helping kids overcome the superficial knowledge of the process in favor of a depth of conceptual understanding.
In our workshops, we make flipbooks to help our teachers understand fractions a little bit better. But what are the most appropriate manipulatives to use to help students gain the conceptual understanding that they need? At what point do I move from a concrete object to a pictorial representation so they’ll understand it more fluidly on paper? These questions and more will be answered in our Fraction February Series. We’ll look specifically at five different manipulatives: pattern blocks, fraction tiles, area models that have been cut out using construction paper, number lines/tape diagrams, and patty paper. We’ll be going through how to use these different manipulatives with all the different parts within the progression of Graham Fletcher’s video, from the beginning interactions with fractions all the way up through the operations with fractions.
