The last star of our Math Mights gang featured in the Math Mights 8-in-1 Flip Chart: Addition Strategies was definitely created with humor in mind. Meet, T-Pops the Traditional.
 As teachers of 21st century math, one of the most common things we hear from parents or people who aren’t in the education field is “Why can’t we just do it the way we used to when we learned it?” Because of this desire to solve problems the “traditional” way, T-Pops is an older character, bald, with a cane and cute bunny slippers. We think of T-Pops like this because when we were younger, traditional problem solving taught us that there was one right answer and one way to get there. T-Pops respects all the other Math Mights and their strategies, and he feels that once you’ve learned all the other ways to solve problems, it’s time to learn his way.
As teachers of 21st century math, one of the most common things we hear from parents or people who aren’t in the education field is “Why can’t we just do it the way we used to when we learned it?” Because of this desire to solve problems the “traditional” way, T-Pops is an older character, bald, with a cane and cute bunny slippers. We think of T-Pops like this because when we were younger, traditional problem solving taught us that there was one right answer and one way to get there. T-Pops respects all the other Math Mights and their strategies, and he feels that once you’ve learned all the other ways to solve problems, it’s time to learn his way.
The T-Pops Approach
We want to teach T-Pops last, because building number sense and the ability to communicate their thinking around other strategies is much more important than solving problems traditionally. Though the traditional method might seem like the “easiest,” we don’t need to race to get kids to understand it. As students develop mathematically, we want them to start by getting lots of experience with number bonds and composing numbers, and learning to solve problems with D.C. We also want them to have experience solving with Abracus and compensation, and then to develop a deep understanding of place value as they learn to do partial sums with The Value Pak. Once they have a foundation of problem solving skills, students can learn to be flexible problem solvers, selecting the most appropriate strategy for their problem. The traditional method certainly has its time and place, but in reality, there are many problems where the traditional method of solving is actually more work than any of the others.
As students develop mathematically, we want them to start by getting lots of experience with number bonds and composing numbers, and learning to solve problems with D.C. We also want them to have experience solving with Abracus and compensation, and then to develop a deep understanding of place value as they learn to do partial sums with The Value Pak. Once they have a foundation of problem solving skills, students can learn to be flexible problem solvers, selecting the most appropriate strategy for their problem. The traditional method certainly has its time and place, but in reality, there are many problems where the traditional method of solving is actually more work than any of the others.
If we teach the traditional method with T-Pops before kids are ready or before they’ve progressed through the developmental stages, we’ve cut them off from communicative thinking. They might know how to go about regurgitating the process of what they’re doing with regrouping and renaming, however, they don’t really understand what they’re doing or have flexibility with the numbers that we need.
 When we were originally thinking of a beach/life raft theme for the Math Mights, the character of T-Pops was a tortoise. Here’s what he looked like originally. He was a slow, older tortoise, moving slow through the traditional method, doing it the old ways and not really thinking about the problems from a different perspective.
When we were originally thinking of a beach/life raft theme for the Math Mights, the character of T-Pops was a tortoise. Here’s what he looked like originally. He was a slow, older tortoise, moving slow through the traditional method, doing it the old ways and not really thinking about the problems from a different perspective.
Manipulatives
As they are learning problem solving strategies, we want kids to interact with both non-proportional and proportional manipulatives. Typically, we start with proportional manipulatives like base-10 blocks because they are more concrete and easier for students to relate to. Once students are comfortable representing problems proportionally, and as they progress through their mathematical development, they move on to using non-proportional manipulatives, like place value discs. The place value discs are considered non-proportional because they are all the same size, but one disc has the number 10 and another disc has 100, so they have different values.
Coins the United States are a good example non-proportional manipulatives. We have a dime, which is small and it’s worth 10 cents, but also have the nickel, which is worth half the amount of a dime but is larger in size.
 When we were learning math growing up, we often went from using proportional manipulatives like the base 10 blocks straight to pencil and paper, skipping the very important step of using non-proportional manipulatives. And usually, we didn’t really understand why we were using base 10 blocks or how what we were doing with the blocks connected to the abstract algorithm of our problem. I remember being taught “just carry the 1” when you have too many. I think I knew it was regrouping, in some ways, but never really understood why it became a 1 or what that 1 represented. Maybe it was a 10 or maybe it was a 100 – who knows! I could have used some non-proportional manipulatives!
When we were learning math growing up, we often went from using proportional manipulatives like the base 10 blocks straight to pencil and paper, skipping the very important step of using non-proportional manipulatives. And usually, we didn’t really understand why we were using base 10 blocks or how what we were doing with the blocks connected to the abstract algorithm of our problem. I remember being taught “just carry the 1” when you have too many. I think I knew it was regrouping, in some ways, but never really understood why it became a 1 or what that 1 represented. Maybe it was a 10 or maybe it was a 100 – who knows! I could have used some non-proportional manipulatives!
Place Value Mat
T-Pops is connected to our new Place Value Mat, which uses the whole number place value discs or the decimal tiles. This tool can help create lots of rich experiences for kids at a conceptual level, making sure they understand what they’re doing when they’re grouping, ungrouping, bundling, unbundling etc. and all those different terms we use when we’re solving a traditional algorithm. (Different terms are used in different programs, so sometimes we call the strategy represented by T-Pops the standard algorithm or traditional algorithm.)
 The tops of the columns in the T-Pops Place Value Mat are not labeled like you might expect with the names of the various places (ones, tens, hundreds, etc.). This is because when you’re using non-proportional manipulatives, the value is written on the discs so it’s not necessary to have it labeled at the top of the column. In fact, it can actually cause more confusion if it is labeled. If you had 4 red tens discs in the tens column, and then it also says tens at the top of the column, it looks like it’s 40 tens instead of the 4 tens, which could be confusing and would definitely impact problem solving. You can read more about the T-Pops Place Value Mat in our recent blog post.
The tops of the columns in the T-Pops Place Value Mat are not labeled like you might expect with the names of the various places (ones, tens, hundreds, etc.). This is because when you’re using non-proportional manipulatives, the value is written on the discs so it’s not necessary to have it labeled at the top of the column. In fact, it can actually cause more confusion if it is labeled. If you had 4 red tens discs in the tens column, and then it also says tens at the top of the column, it looks like it’s 40 tens instead of the 4 tens, which could be confusing and would definitely impact problem solving. You can read more about the T-Pops Place Value Mat in our recent blog post.
We’ve been working with some kids in schools lately that don’t really understand place value, so for those students, I have actually labelled those columns with dry erase marker to scaffold them into that understanding. But, I warn them that the labels are like training wheels; use them for as long as you like, but at some point you just have to let go!

We can regroup at the top or we can regroup at the bottom, but for the traditional algorithm, we chose to follow a strategy called “grouping at the bottom.” When we’re working with addition problems and T-Pops, often students will talk about “carrying the 1.” You can’t really carry it anywhere! Instead, students need to learn to rename the number with place value. For example, if you have 12, that’s actually 1 ten and 2 ones. Another example: If I had 62 + 8. 62 is 6 tens and 2 ones. I add the 2 ones to the 8 ones, to get 10 ones. I still have 6 tens, and the 10 ones can be renamed into 1 ten. So, I have 7 tens all together and the answer is 70.
It’s perfectly ok if kids want to regroup on the top. For kids who have been regrouping at the top for a long time, it can be hard for them to make the switch to regrouping at the bottom, however, it can help students really see the numbers more closely. In talking to many of our second grade teachers (since they’re the ones to introduce the traditional method of addition), they find that students really benefit from learning how to regroup at the bottom because they can actually see the numbers more accurately. As students are acting out the problems with the place value mat, they can really see what they’re doing and how it matches the traditional algorithm.
When they use the Place Value Mat to solve addition problems the traditional way, students build their first addend on the mat. Let’s say we have 27 + 15. They’re going to build their first addend on the T-Pops place value chart. They’ll put their 2 tens and 7 ones. In the bottom area, they’ll build their second addend, the 15, which is worth 1 ten and 5 ones. Most people don’t realize that the mat is actually designed to be a 10 frame, and so the numbers should be loaded onto the mat in the same way we use that 10 frame. So, we start by moving the ones onto the mat. There are 12 ones, so we can rename that into 1 ten and 2 ones. Then, we can add 20 + 10 + 10 to equal 40 and then add the 2 ones to get 42.
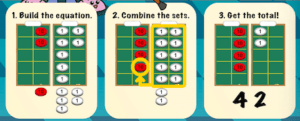
While kids are using the T-Pops Place Value Mat, make sure that they are also recording what they’re doing on the dry erase board part of the mat. Every time you make a move on the mat, T-Pops wants to make sure you’re understanding what you’re doing physically by showing what you’re doing in the algorithm.
Although T-Pops is our oldest citizen in Mathville, he’s very respectful of other characters, knowing that it takes patience and time to get where “we used to be.” We know developmentally that if we rush to teach T-Pops we are undoing the development of children. This message is really important to get out to parents, because they don’t really understand the developmental levels of reasoning and why we’re teaching with number sense. We want kids to be able to explain their thinking, which will help them in 21st century learning and for the jobs they will have at some point in the future.



